Turing-Complete Rule 110 on Bitcoin

Getting your Trinity Audio player ready...

This post originally appeared on Medium, and we republished with permission from Xiaohui Liu.

We have implemented Rule 110 on Bitcoin. Similar to two-dimensional cellular automata (CA) Conway’s Game of Life, Rule 110, a one-dimensional CA, is also Turing-complete. By deduction, we have shown Bitcoin is Turing Complete, once again.

Rule 110

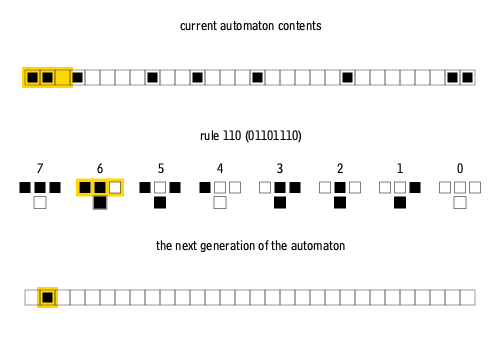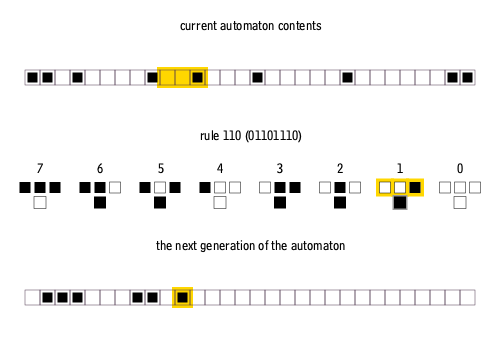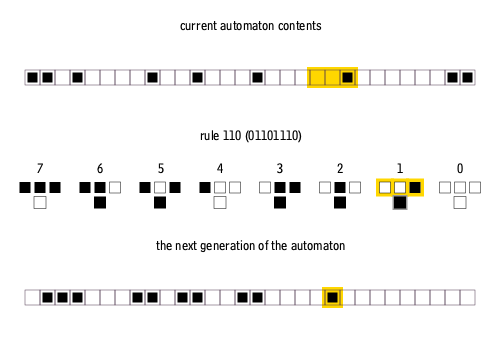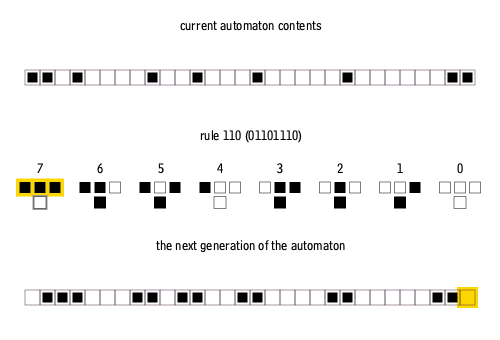
The Rule 110 cellular automaton is a 1-dimensional elementary CA, where a linear pattern of 0s and 1s evolves according to a simple set of rules. Whether a point in the pattern will be 0 or 1 in the new generation depends on its current value and on those of its two neighbors. The Rule 110 has the following set of rules:

The name “Rule 110” is based on the fact that this rule can be summarized in the binary sequence 01101110, corresponding to the decimal value 110.

Turing-Complete

Despite its simplicity, Rule 110 is Turing-complete, as proven in Universality in Elementary Cellular Automata (Cook 2004). This implies that, in principle, it can simulate any calculation or computer program. Rule 110 is arguably the simplest known Turing-complete system.

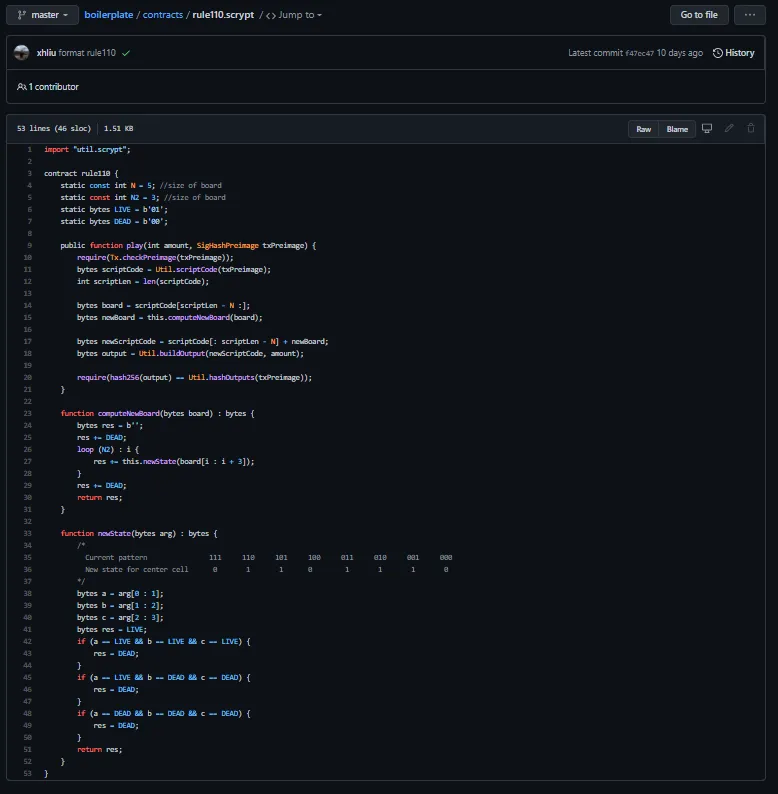
Implementation

We have implemented Rule 110, in a similar approach to implementing Game of Life.