Scalable peer to peer tokens on Bitcoin: Solve the back-to-Genesis problem using recursive SNARKs

Getting your Trinity Audio player ready...

This post was first published on Medium.

This is an implementation of nChain’s solution¹.

The Back-to-Genesis Problem

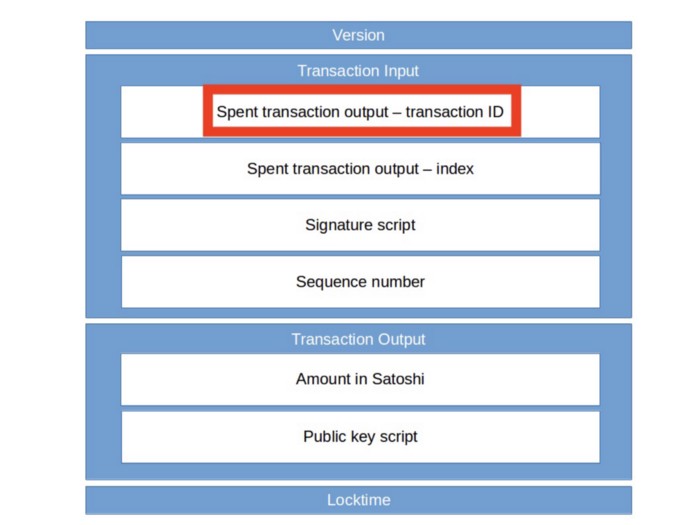
Tokens on Bitcoin are typically stored in UTXOs. When a supposed token transaction is received, a user needs a way to efficiently and quickly check its authenticity. A major part is to decide if it links to certain genesis transaction, where the token is issued.

In a basic form, the Back-to-Genesis (B2G) problem boils down to: given a transaction, is it linked to certain genesis transaction in an unbroken chain of transactions?

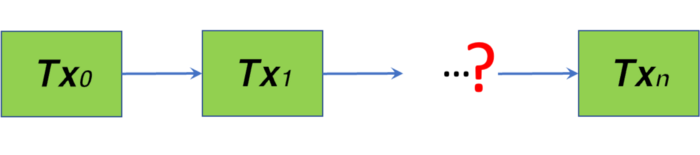
All tokens on Bitcoin today have to rely on some trusted third-party to address the problem, since it becomes computationally challenging for a light-weight user to verify himself when the chain is excessively long². For instance, DotWallet’s Badge tokens use a token indexer and Sensible tokens use an oracle. This third-party reliance hurdles token adoption on Bitcoin, since it is not as scalable and SPV-friendly as native bitcoins.

Our previous proposal attempts to solve the problem without any third party. However, the size of a token transaction grows exponentially when the chain grows, severely limiting its usage in practice.

Recursive SNARKs

Recall in a recursive SNARK, specifically incrementally verifiable computation (IVC), we want to prove that a function F applied n times to initial input z₀ yields zₙ.

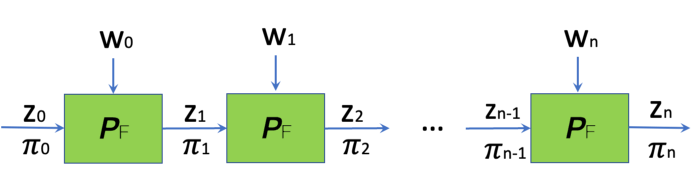
In each step, zᵢ is the public input and wᵢ the private input (i.e., witness).

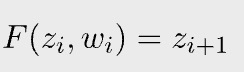
Each step produces a new proof. In step i, the prover algorithm computes 𝛑ᵢ that proves all steps up to i are correct, using only local information from the last step and current step as shown below. Crucially, it does not trace all the back to step 0, while still being able verify all steps since step 0 are correctly executed.

Prover algorithm: compute proof incrementally

Applying recursive SNARKs to B2G

IVC naturally leads to an elegant solution to the B2G problem.

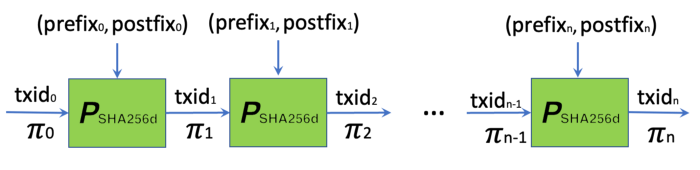
IVC in B2G

Concretely, IVC is instantiated as follows:

• zᵢ: txidᵢ, the transaction id of i-th transaction in the chain
• wᵢ: the rest of i-th transaction. We divide into it into two parts: prefixᵢ and postfixᵢ, representing what comes before and after txidᵢ.
• function F: the txid of a transaction is the double SHA256 of it and the (i+1)-th transaction spends the i-th transaction, its txid and thus F is calculated as below:

txid is the red box part, prefix/postfix is everything before/after it, respectively. || is concatenation.

A Transaction

We can now prove a transaction descents from a given transaction by verifying a single short proof regardless of the length of the transaction chain, without tracing all the way back.

A simple NFT token protocol

Let us construct a simple NFT token using the above approach. An NFT is minted in an issuance transaction, a.k.a., a genesis transaction. For simplicity, let us use only only one input and one output in each transfer transaction³.

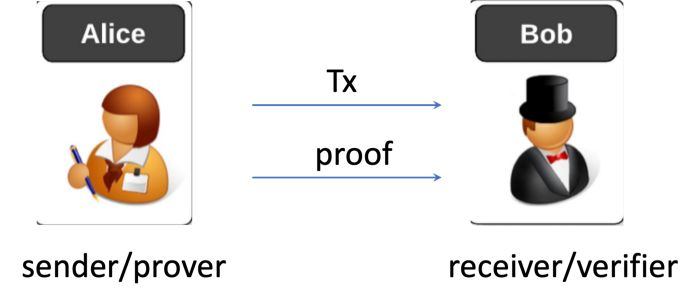
When Alice transfers an NFT to Bob, she constructs a transaction with Bob as the receiver and hands it to Bob directly off chain. Thanks to the peer-to-peer nature of Bitcoin, she also sends an SNARK proof along with the transaction. Alice can generate the proof without tracing to the genesis transaction as we explained earlier.

Bob only accepts the NFT if both checks pass:

1. he validates the transaction using SPV, similar to a regular bitcoin payment
2. he verifies the proof⁴.

Without the first check, an attacker can create alternative transaction chain originating from the genesis transaction, but is not on the Bitcoin blockchain. Without the second check, the token transaction may not link to the genesis transaction.

The proof is of constant size of only a few KBs and can be verified within seconds regardless of the chain length, incurring negligible overhead. The token transfer is effectively instant, just like a regular bitcoin payment.

Prover time

The most time-consuming part of recursive SNARKs is generating a proof, which can be up to a minute on a resource-constraint device. To enable instant token transfer, a proof can be pre-computed as soon as a token is received by Bob, so it is ready when Bob transfers it to the next owner. In case where Bob needs to send the token to Charlie immediately after receiving it from Alice, he can send the old proof received from Alice and have Charlie verify the last two links in the transaction chain, without generating a new proof as a fallback.

Implementation

We have implemented the recursive SNARK using snarkyjs as below.

Recursive B2G Proof

To start, we need to first compile the program to get the verification key. Note that there is no trusted setup.

The key can be made public at a central registry associated with the genesis transaction, or it can be placed in another output of the genesis transaction.

The genesis method starting from Line 5 is called to generate the initial proof, which simply checks txid0 is the genesis transaction id at Line 9.

The transfer method starting from Line 13 is called to generate a new proof attesting to:

• the last proof is valid at Line 17
• the current transaction spends the last transaction at Line 18 and 19.

Finally, we can verify a proof against the verification key.

The full code can be found in this Github repo.

Summary

We only present a simple NFT example using recursive SNARKs. It can be extended to a directed acyclic graph (DAG), rather than a chain of transactions. It may also be extended to fungible tokens or any other use cases where a user needs to efficiently ensure a transaction can be linked to some ancestor transaction.

Acknowledgements

We thank nChain for sharing the original idea of applying recursive SNARKs to the B2G problem. We also thank Gregor Mitscha-Baude of O(1) Labs for helping with the SHA256 circuit implementation.

***

NOTES:

[1] WP1590 Transaction Chain Proof, M. S. Kiraz and O. Vaughan, patent pending GB2200400.6.

[2] In a more general form, transactions form a directed acyclic graph (DAG), making solving B2G even more computationally intensive.

[3] This can be enforced in a smart contract or the SNARK circuit, or both. In the former, we can use the OP_PUSH_TX technique to limit the number of inputs and outputs in all transactions descending from the genesis transaction. For example, we can enforce that any NFT transaction has two inputs and one output. The second input covers transaction fee.

[4] Optionally, the proof verification can be done on chain. It only requires implementing the verifier in the snarkyjs proof system, similar to the Groth16 verifier we have implemented.

Watch: The BSV Global Blockchain Convention presentation, Smart Contracts and Computation on BSV

https://www.youtube.com/watch?v=c_zAlkImgTU