|
Getting your Trinity Audio player ready...
|
This post was first published on Medium.
Previously, we have proved one knows some mathematical secret using zero knowledge proof (ZKP), without revealing the secret itself. The secret knowledge include:
- a private key corresponding to a public key in ZK puzzles
- a hash preimage to a public digest in ZK key-statement proof
- a ciphertext is the encryption of a private key in ZKP-based escrow.
While useful in their specific applications, these ZKPs cannot be applied to arbitrary mathematical functions. Overcoming these limitations, a zk-SNARK (zero-knowledge Succinct Non-interactive ARguments of Knowledge) is a protocol designed to generate a ZKP for any mathematical function. The generated proof is “succinct” and “non-interactive”: a proof is only a few hundred bytes and can be verified in constant time and within a few milliseconds, without needing to ask additional questions of the prover. Together, these properties make zk-SNARK especially suitable for blockchains, where on-chain storage and computation can be expensive and senders often go offline after sending a transaction. Anonymous cryptocurrency Zcash and the smart-contract platform Ethereum are among its notable early adopters, among others.
zk-SNARK
A zk-SNARK consists of the following three algorithms: G ,P, andV.
https://twitter.com/ChrisLundkvist/status/799807876982251520?s=20&t=-Pa3US30hCFPMskd-MyhiA
Key Generation
A key generator G takes a secret parameter λ and a function C, and produces a proving key pk and a verification key vk. Both keys are made public.
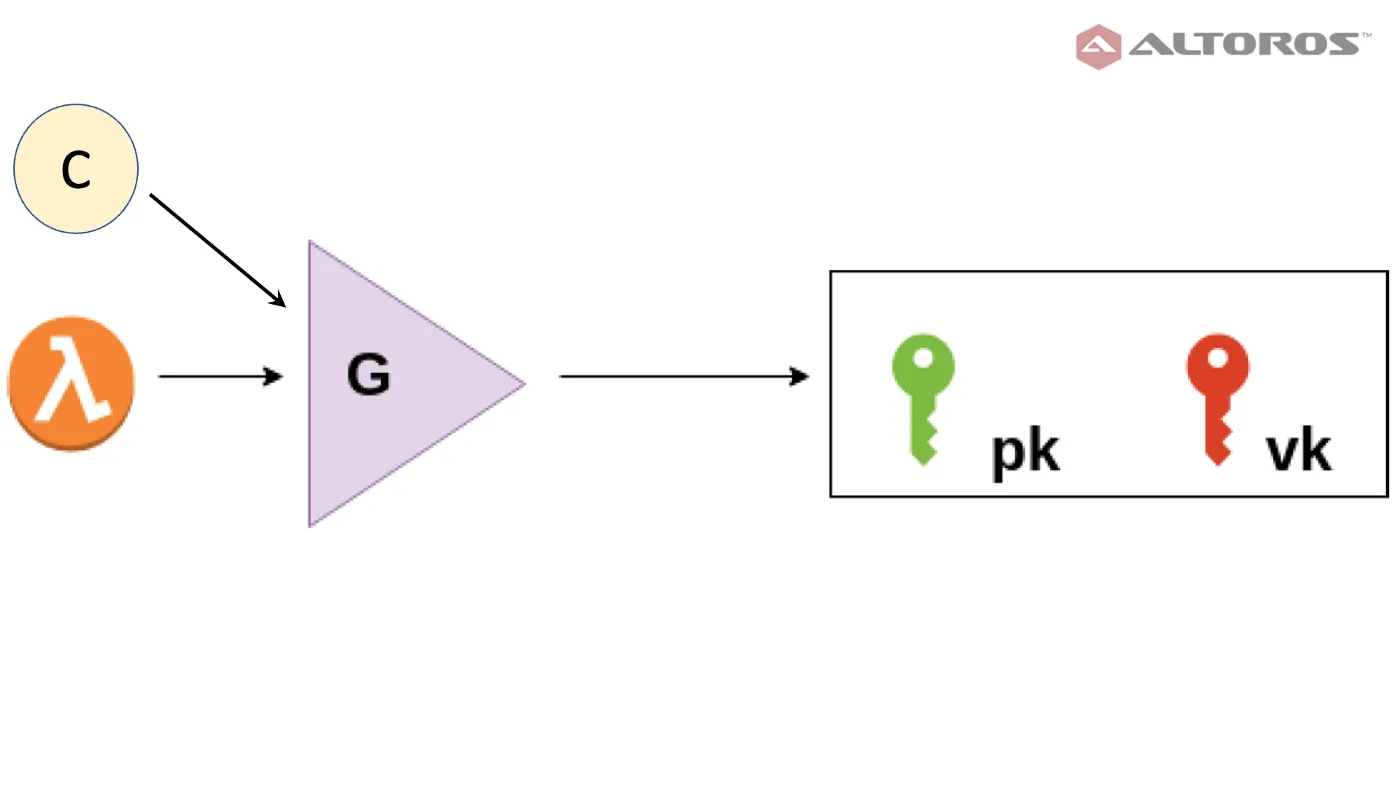
C is a boolean function (also called a program or circuit) that takes two inputs: a public input x and a private input w (aka, witness). For example, C can be a function that checks if w is the sha256 preimage of the digest x.
C(x, w) = sha256(w) == x
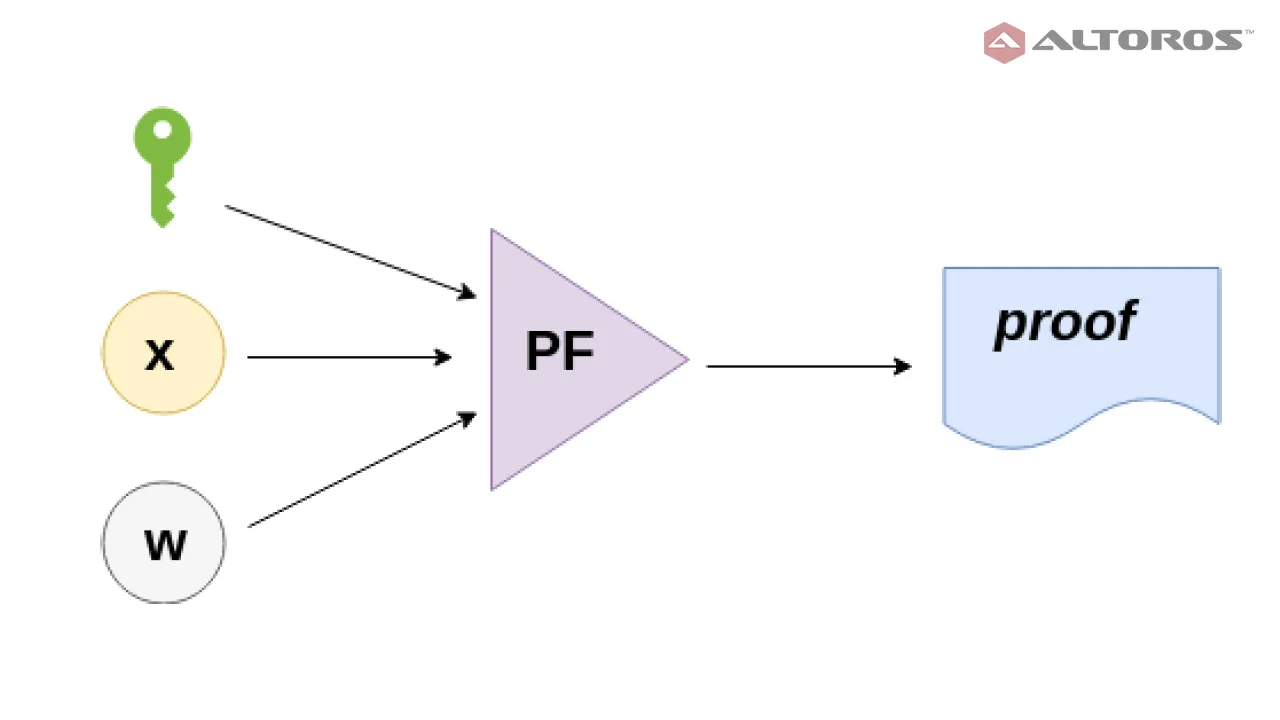
Prover
The prover P takes as input the proving key pk, a public input x and a private witness w to produce a proof that the prover knows a witness w that makes C(x, w) evaluates to true.
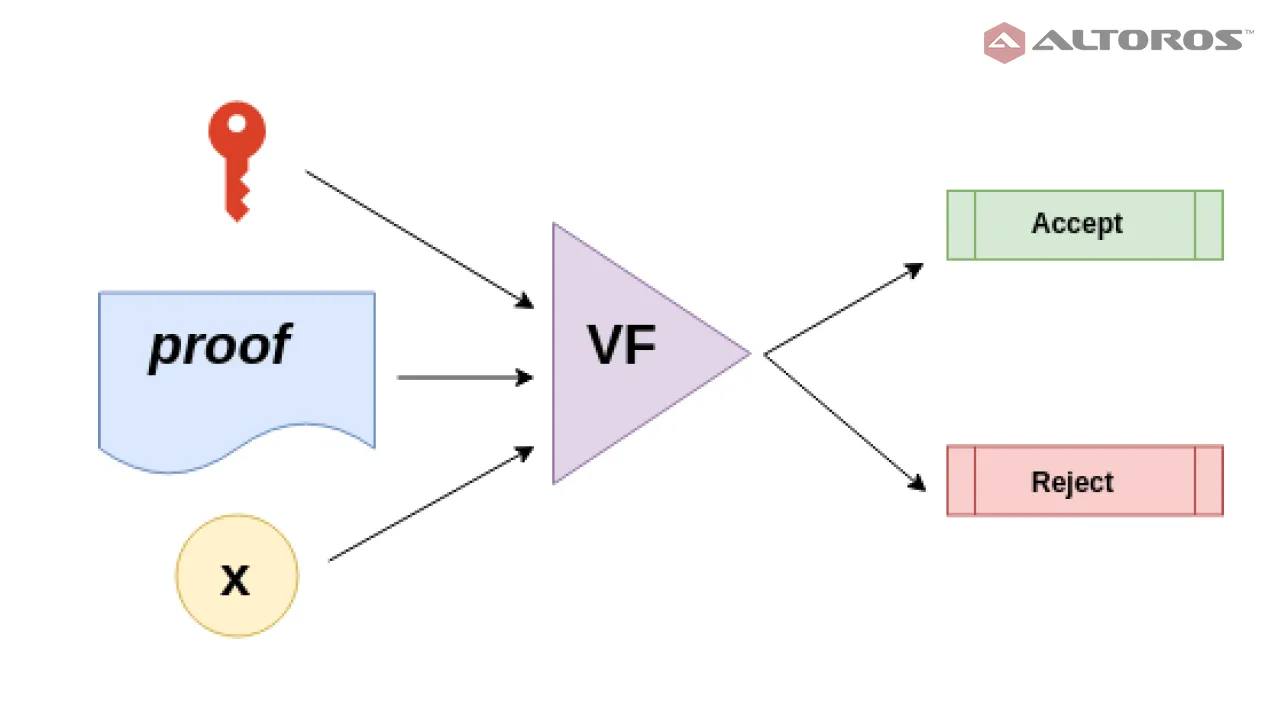
Verifier
The verifier V takes verification key vk, the proof, and the public input x and accepts the proof only if it is produced with the knowledge of witness w¹.
Implementation
When zk-SNARKs are used in blockchains, both the key and proof generation are executed off-chain. Only the general verification algorithm is run inside a smart contract on chain.
There are multiple schemes of zk-SNARKs in the literature. We implement the most widely used scheme Groth16 due to its small proof size and fast verification.
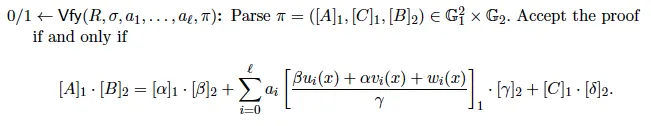
The full code is listed below, based on our elliptic curve arithmetic and pairing libraries.
Contract ZKSNARK
It is worth noting that the proof size (Line 23–27) and the number of pairings (Line 43–44) are constant, regardless of how complex the function C being proved is.
Summary
zk-SNARK is a powerful primitive for blockchain privacy and scalability. Today we only showed what zk-SNARK is and how to implement it on Bitcoin. We will explore how to use it in the near future. Why and how it works internally, which is quite math heavy, is beyond the scope of this single article. There are many excellent tutorials such as this series and this paper.
***
NOTE:
[1] There is an exception. Anyone knows the secret parameter λ used in the generator can generate fake yet valid proof without knowledge of witness. That is why it is called toxic waste. It must be discarded after the trusted setup phase.
Watch: The BSV Global Blockchain Convention presentation, Smart Contracts and Computation on BSV
https://www.youtube.com/watch?v=RzSCrXf1Ywc&t=6154s

 07-15-2025
07-15-2025 





