Verifiable Delay Functions on Bitcoin

Getting your Trinity Audio player ready...

This post was first published on Medium.

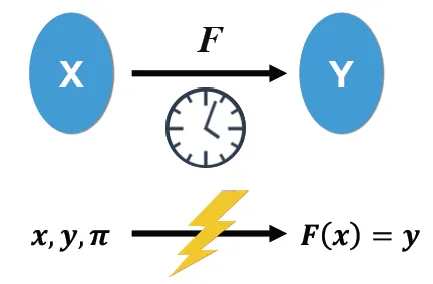
A Verifiable Delay Function (VDF) is a function that takes a significant amount of sequential computation to evaluate, but is fast to verify. We have implemented it on Bitcoin for the first time. VDF, as a cryptographic primitive, can be used to build a plethora of new applications, such as public random beacons, computational timestamping, and proofs of data replication.

VDF

Motivations

Random beacon on chain

Achieving randomness is hard in a blockchain since everything is deterministic and public. A classical example is a betting smart contract between two parties, where one party wins if the next block hash is even, and the other wins if it is odd. A miner can cheat this contract by playing it and, at the same time, ignoring any new block that makes him lose the bet.

A VDF alleviates this problem by demanding the randomness comes not from the block itself, but from a VDF of it. By tuning the VDF to take a long time to compute, say one hour, a miner is disincentivized to cheat by forfeiting mining rewards in found blocks of the next hour, since it is bigger than the bet amount.

Lottery

In a similar example, Alice, Bob, and Charlie would like to play a round of lottery, which requires them to generate a random number jointly to decide the winner. In a naive approach, each of them publishes a random number. Once all participants have done so, they compute a hash of the sum of the published numbers.

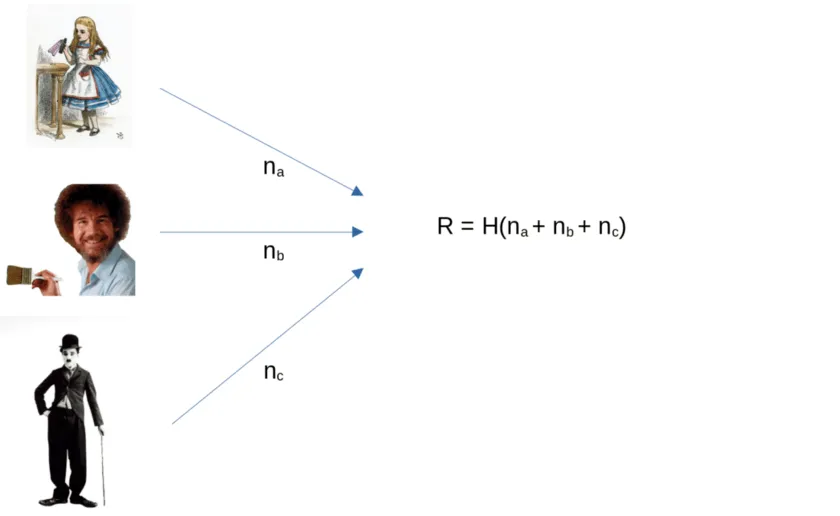
The problem is that the last one to submit his number can control the outcome. For example, if Alice and Bob have already submitted their values, Charlie can just try to calculate the result using different numbers until he finds a number that produces the outcome he wishes.

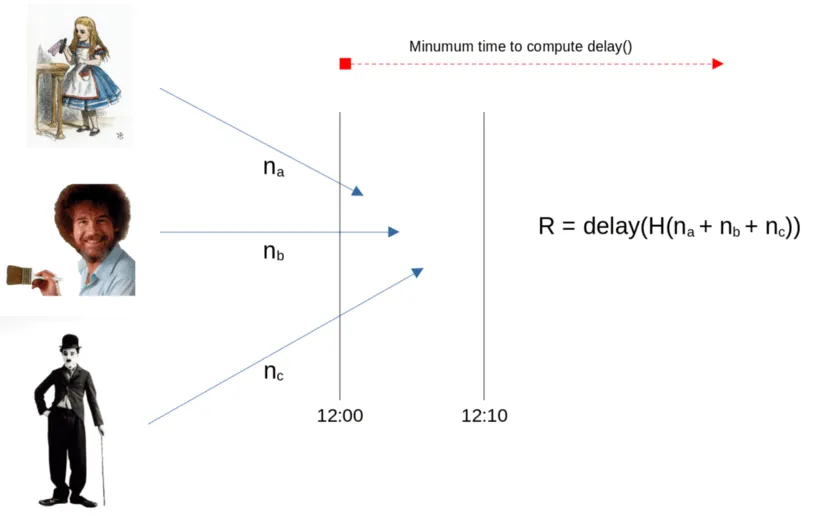
To overcome this problem, we introduce a delay using VDF. Let us say participants must submit their numbers between 12:00 to 12:10. After all the numbers are submitted (or the deadline has passed), they again get hashed, and a VDF is evaluated on the resulting hash that takes a longer amount of time to evaluate than 10 minutes, say, one hour. Now Charlie could not cheat as the time for evaluating the result is longer than the submission window.

Formal definitions

A valid VDF f must have the following properties:

• Sequential: anyone can compute f(x) in t sequential steps. Note it is imperative the computation cannot be parallelized. This ensures that an attacker is not able to just speed up the computation significantly by utilizing more resources. The time of computation is limited solely by the speed of a single thread of execution.
• Efficiently verifiable: given the output y, any observer can verify that y = f(x) in a short amount of time, specifically log(t).

VDFs are a way to provably slow things down. They introduce a forced time delay to an output so that malicious actors can’t influence it by predicting future values.

VDF vs Proof of Work

VDFs and Proof of Work (PoW) are both hard to compute, but easy to verify. The fundamental difference is that PoW can be parallelized, while VDFs cannot.

Implementation

Since a VDF is efficiently verifiable, we can verify it in a smart contract. We have implemented a verifier for a popular VDF developed by Wesolowski.

The VDF could be represented as the following function:

x is the input value, T is the delay parameter known publicly and determines the duration of the delay, and y is the output.

To compute x^ 2 ^ T, we will have to compute sequentially x^ 2 ^ i with i from 0 to T. Crucially, the repeated squaring computation is not parallelizable.

To make it efficiently verifiable so that a verifier doesn’t need to follow the full T steps again, the following interactive protocol is run. The protocol can be made non-interactive using the Fiat–Shamir heuristic.

The verifier is implemented below.

The full code, along with tests, can be found on GitHub.

Watch: The BSV Global Blockchain Convention presentation, Smart Contracts and Computation on BSV