Private non-interactive bounties for general computation on Bitcoin

Getting your Trinity Audio player ready...

This post was first published on Medium.

How to securely outsource any computation

We present a novel bounty mechanism that can outsource arbitrary computation securely and privately on a blockchain. The exchange of solution and payment is atomic and trustless: either the bounty maker learns the solution and the collector gets the rewards, or neither happens. The maker deploys a smart contract that releases funds if and only if a solution is provided. To prevent the solution from leaking, it is encrypted with a key that only the two parties know. To validate the encrypted solution, Zero-Knowledge Proof (ZKP) is used to prove the solution encrypted is valid and it is encrypted using the right key while keeping it confidential.

To our best knowledge, it is the first-ever and only way to securely outsource any computation without a trusted third party.

The fair exchange problem

A buyer wants to know the solution to a computational problem, such as a Sudoku puzzle. She does not want to or cannot solve it herself, so she outsources it by making a bounty that pays a seller offering a solution.

If the buyer pays first, the seller may not tell him the solution.

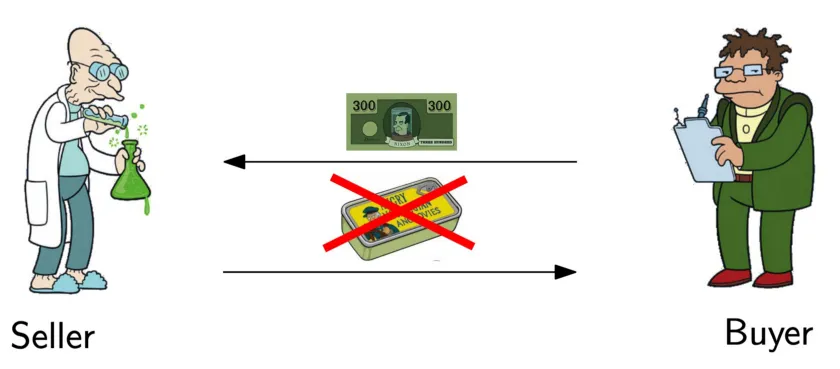
Similarly, if the seller discloses the solution first, the buyer may refuse to pay.

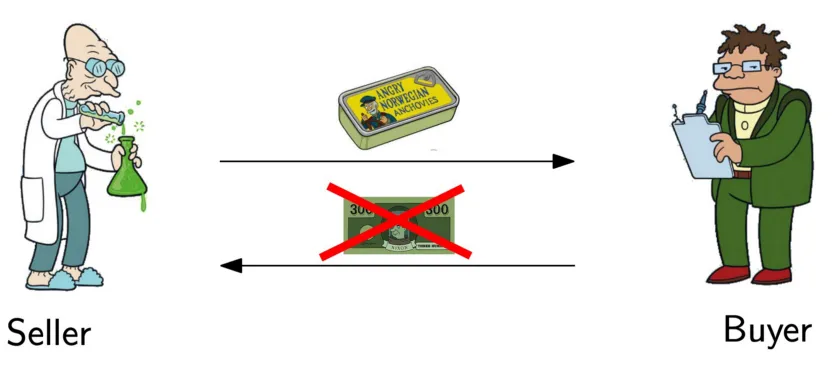
This is the canonical fair exchange problem. It is trivial to solve if there exists a third-party escrow that both trust. Several attempts have been made to solve it without an escrow.

First attempt

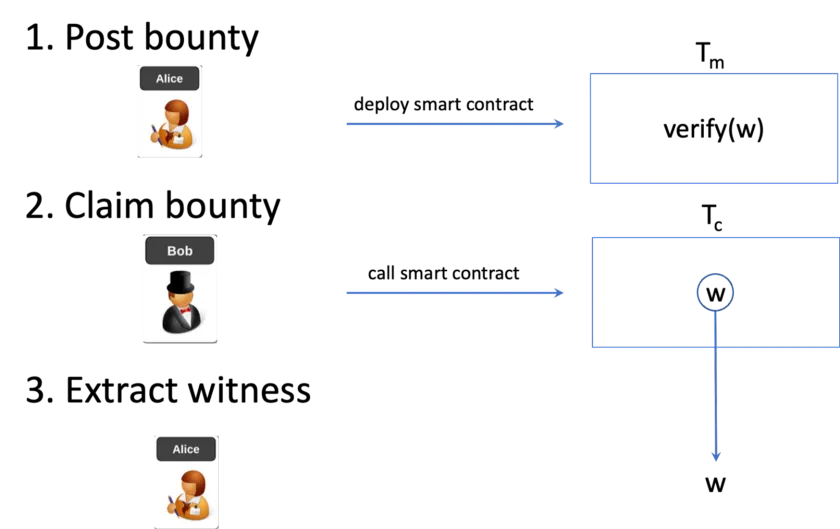
A naive approach is to simply deploy a bounty smart contract on a public blockchain for the problem, as we have done to outsource the Travelling Salesman Problem. It consists of three steps as Fig. 1 depicts:

1. A bounty maker Alice places a bounty transaction Tm containing a smart contract that pays for a witness w satisfying a problem represented in a circuit C, i.e., C(w) evaluating to true.
2. A bounty collector Bob submits w to the bounty transaction in another transaction Tc.
3. The maker Alice extracts w from the above transaction.

Anyone can attempt to collect the bounty by submitting a solution to the smart contract. The smart contract pays the collector after it validates a proposed solution that indeed solves the problem. Due to the transparent nature of a public blockchain, this suffers from two drawbacks:

• an attacker, such as a malicious miner, can intercept a collector’s transaction, extract the solution, and create a competing transaction to claim the bounty himself, without solving the problem.
• anyone can learn the solution by observing the solution posted on chain. This is problematic if the bounty maker intends to keep the solution private, which he pays for.

Second attempt: Zero Knowledge Contingent Payment (ZKCP)

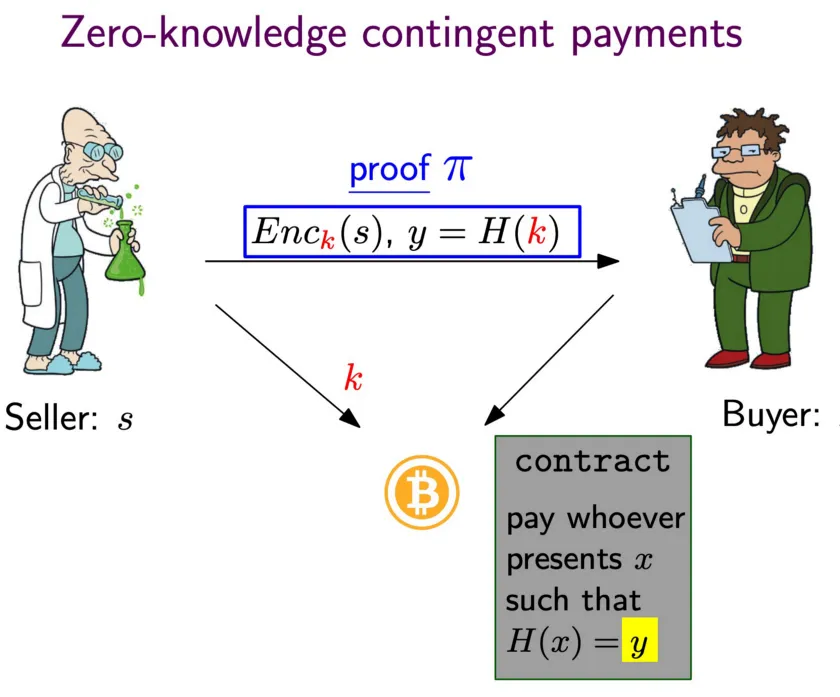
ZKCP allows a buyer to purchase a solution from a seller using Bitcoin that does not require trusting anyone. It consists of two steps:

1. Using ZKP, the seller convinces the buyer that a hash preimage k is the encryption key to a valid encrypted solution s off chain, without disclosing the solution.
2. The buyer then locks bitcoins in a payment transaction to the seller, which can only be redeemed if the seller provides the right preimage, which the buyer uses to decrypt the solution.

ZKCP also has drawbacks:

• the buyer can abort after verifying the ZKP after step 1 and the seller is not paid even if he has spent considerable resources to solve the problem.
• It requires interaction between the seller and buyer, which is not ideal in a blockchain setting, where users often go offline after sending a transaction.

Our solution

Our bounty mechanism addresses all the aforementioned issues and enjoys the following salient properties.

1. Non-interactive: a bounty maker creates a bounty for solving a computationally hard problem by sending a single transaction to the blockchain.
2. Open: anyone can collect the bounty in a follow-up transaction as long as he has the solution, and the collector is unknown at the time of bounty creation.
3. Extractable: the bounty maker is guaranteed to be able to extract the solution from the bounty collecting transaction.
4. Secure: malicious eavesdropping parties cannot claim the bounty even if they intercept the collecting transaction.
5. Private: an outsider cannot learn the solution by observing the blockchain.

The difficulty in realizing a bounty meeting all these requirements arises because the identity of the user who solves the problem is unknown at the time the bounty is posted. In Fig. 1, a malicious attacker, such as a miner, can eavesdrop Tc, obtain the witness, and redeem the reward himself, since the smart contract in Tm allows anyone with w to redeem. Also any third party can observe Tc on the blockchain and learns the secret w, which the bounty maker pays for and may wish to keep private. A way is needed to encrypt and hide w, while still ensuring C(w) is true.

To prevent these attacks, w is encrypted with a shared key using a symmetric encryption. It is derived from an Elliptic Curve Diffie–Hellman (ECDH) key exchange, as Fig. 2 illustrates. Alice’s public key QA is published in Tm. Bob has to use QA to derive the shared key. He exposes his public key QB in Tc, which Alice uses to derive the same shared key and decrypt the encrypted solution to obtain w.

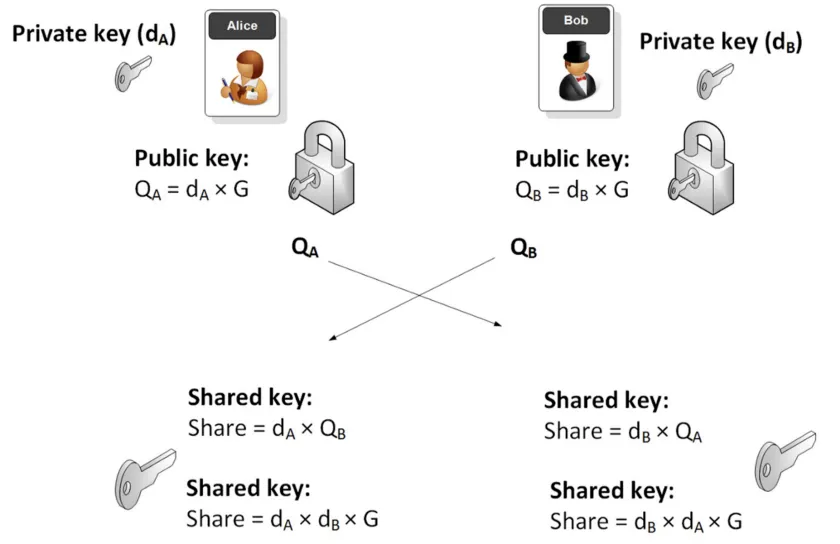
ZK Circuit

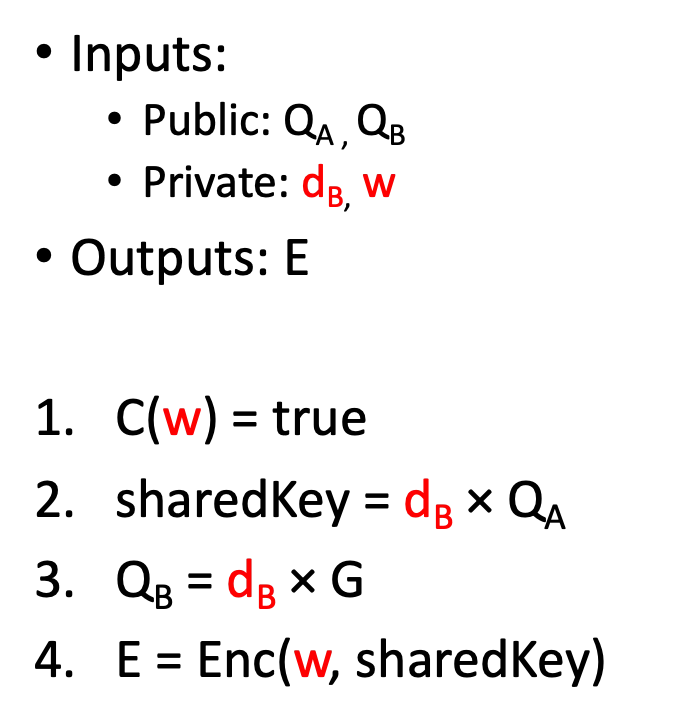
The smart contract in Tm verifies the proof in Tc attesting to the composite circuit shown in Fig. 3. It takes several inputs, including the private witness w, and outputs the witness encrypted with the shared key. Step 1 ensures the w is valid, and the rest validates w is encrypted with the right shared key, so that Alice can decrypt it. Step 2 uses ECDH to derive the shared key.

Enc() in step 4 can be any symmetric encryption. In practice, a ZKP-friendly encryption such as Poseidon encryption is desired for efficiency.

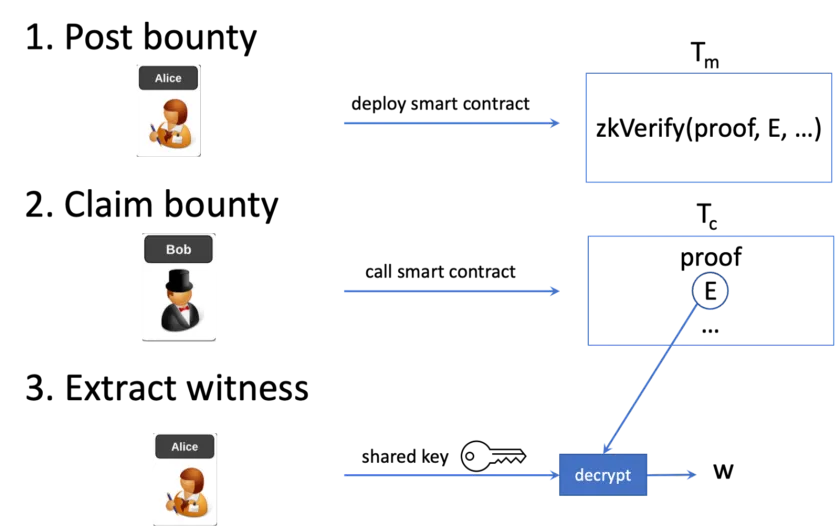
Final workflow

The final improved bounty mechanism is depicted in Fig. 4.

1. A bounty maker Alice places a bounty transaction Tm containing a smart contract that releases funds if a proof attests that E is w encrypted.
2. A bounty collector Bob solves for w and encrypts it with a shared ECDH key, based on his private key and Alice’s public key. He generates a ZK proof and submits a transaction Tc to claim the bounty, containing the proof and ciphertext E.
3. Alice derives the same shared ECDH decryption key, based on her private key and Bob’s public key. She decrypts E in Tc and gets w.

If an attacker intercepts Tc and changes the recipient, the proof will be invalidated since it is bound with Bob’s public key. The attacker cannot redirect and steal the bounty. The proof is akin to a digital signature used in regular payment transactions, protecting against tampering. Also, the attacker cannot see the witness since it is encrypted.

In practice, a deadline will be added to the bounty. In case no one claims it within a certain time, Alice can get her money back.

How to get Bob’s public key

Bob’s public key QB, sender of the claiming transaction, is readily available in an account-based blockchain such as Ethereum. Ethereum’s Solidity programming language exposes it in the global transaction variable tx.origin or msg.sender.

In Bitcoin, we extract QB based on a technique called OP_PUSH_TX. OP_PUSH_TX allows the smart contract (in Tm) to access the spending transaction (Tc), thus enforcing where the bounty goes to the collector’s public key QB, used in ECDH to derive the shared encryption key[1].

Bitcoin vs. other blockchains

This bounty mechanism can be applied in many blockchains. In blockchains where an unconfirmed transaction can be delayed by a later transaction with a higher fee, such as BTC and Ethereum, it is possible for the bounty issuer Alice to intercept Tc, decrypt and fetch the witness w. She can create a competing collecting transaction using w to frontrun Tc with a higher transaction fee before it is mined into a block. On Bitcoin, this is extremely unlikely since transactions are processed on a first-come, first-served basis.

Trusted setup

There are two categories of ZKPs: those that require a trusted setup and those that do not. In many cases, the latter is preferred because it tends to be more efficient. If Bob conducts the setup, he can create a fake proof and steal the bounty without solving for w. Since no third party can be trusted, Alice has to conduct the setup.

Different from ZKCP, it is not a problem here if Alice maliciously manipulates the setup to learn part or entirety of the witness from the proof, by breaking the zero-knowledge property the ZKP used[2]. She will decrypt the proof to get the witness anyway. For additional security, Bob can perform additional checks of the setup to ensure it is carried out by Alice honestly and the Common Reference String is well formed. He can also verify his proof does pass validation by running the verifier smart contract locally and only broadcast Tc after it passes.

Potential use cases

The invention opens up numerous ways to outsource arbitrary practical computational problems to the general public. Anyone, who submits a solution first, is guaranteed to get paid. Below are just a few examples.

• Mining: a mining pool outsources hashing by offering to pay any miner who finds a nonce that makes a given block header hash meeting the share difficulty target. The miner does not have to trust the pool for payout, as in a traditional mining pool. The payout is trustless and instantaneous.
• Machine learning: a business wants to train a machine learning model, such as natural language processing or linear regression, on a given dataset to improve its users’ experience. It outsources the training in the hope of finding the most accurate model at an affordable price tag without a centralized platform like Kaggle.
• Provable high-resolution image: a user of a website likes an image, which is of low resolution and is just a preview. He wants to purchase the high-resolution copy, probably downsizing to the preview.
• Traveling salesman problem: a logistics company wants to find the shortest route to efficiently deliver packages to a list of recipients, to minimize gas costs.
• A Sudoku puzzle: Alice is an avid fan of Sudoku and has a puzzle she is stumped on for hours. She gives up and posts a bounty to whoever provides the solution to the puzzle.

Rapid technological advancement in ZKPs has made it possible to prove many statements of practical applications. We will demonstrate how to leverage this bounty mechanism to solve practical problems soon. Stay tuned!

Acknowledgements

We thank ZeMing Gao for reviewing an earlier draft of this article and offering constructive feedbacks.

[1] In case addresses derived from hashes of public keys are used in transactions, instead of public keys themselves, QA and QB are replaced with Alice’s and Bob’s addresses, and additional steps are needed to ensure addresses are derived from public keys.

[2] WI Is Not Enough: Zero-Knowledge Contingent (Service) Payments Revisited

Watch: The BSV Global Blockchain Convention presentation, Smart Contracts and Computation on BSV