Programmable zero knowledge proofs using zk-SNARKs: part 1

Getting your Trinity Audio player ready...

This post was first published on Medium.

Prove Knowledge of a Private Key Without Signatures

In theory, a zero-knowledge proof (ZKP) can be constructed for any mathematical problem¹, without revealing this solution. In practice, developing a ZKP for a problem often requires the invention of a whole new cryptographic algorithm. It has no standard recipe and requires extensive and in-depth knowledge of cryptography. For example, ZK puzzle involves ∑-protocols and ZK key-statement proof Pedersen commitments and Fiat-Shamir heuristic.

zk-SNARKs standardize ZKP generation for arbitrary problems. One only needs to express the original problem to be proven in ZK format, such as domain-specific language (DSL) Circom or Zokrates. All the rest is handled by the generic zk-SNARK framework, hiding all the complexities of the underlying cryptography.

Prior to zk-SNARKs, constructing ZKP for a new problem is akin to building a new ASIC whenever a new ZKP application needs to be devised. zk-SNARKs allow building the new ZKP by simply programming a general-purpose “ZK CPU.” The former requires one to be a cryptographer, while the latter only requires one to be a programmer, greatly lowering the barrier to entry of ZKPs.

To demonstrate the power of this paradigm shift, we use it to construct the most popular ZKP: knowledge of the private key for a given public key, aka, discrete logarithm.

ZKP of Knowledge of a Private Key

To transfer bitcoins locked to a public key/address, an owner has to show he knows the corresponding private key. But he cannot simply disclose it, otherwise bitcoins can be stolen. This is done with a digital signature, a form of ZKP². We show an alternative way to achieve the same using zk-SNARK.

In Bitcoin, a public key Q is simply the private key d multiplies the generator G.

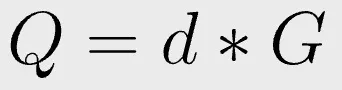
The following Circom code implements scalar multiplication over Bitcoin’s elliptic curve secp256k1. We can easily use it prove Q is the public key of d:

• Set the input scalar at Line 3 to d: note it is private and thus remains confidential
• Set the input point at Line 4 to G
• Set the output at Line 6 to Q.

Scalar Point Multiplication. Credit: 0xPARC/circom-ecdsa

We use the standard double-and-add algorithm, for ease of exposition. A more efficient algorithm can be found here. The main loop occurs from Line 33 to Line 65. We use Secp256k1AddUnequal at Line 42 for point addition, and Secp256k1Double at Line 43 for point doubling. We keep doubling at Line 355–358 in each iteration. We also add if the current bit is set.

Once we have the Circom code, we can use our generic zk-SNARK library to prove knowledge of a private key, while keeping it secret. We have demonstrated the knowledge without a digital signature!

Stay tuned for more examples of ZKPs leveraging the programmability of zk-SNARKs.

Acknowledgements

This article is inspired by this excellent write up.

***

NOTES:

[1] In fact, ZKP can be constructed for any NP problem.

[2] We use ZK loosely here.