Zero-knowledge key-statement proof

This post was first published on Medium.

nChain white paper #0488 titled “Zero-knowledge key-statement proofs” introduces a zero-knowledge proof (ZKP) that proves a private key, corresponding to a given public key, satisfies certain requirements, while keeping the private key confidential. We have implemented it and applied it to purchasing bitcoin vanity address trustlessly. It can be generalized to a wide range of applications, where secret information can be purchased between mutually distrusting parties without a trusted third party.

Zero-Knowledge Key-Statement Proof

As we have introduced before, a zero-knowledge proof lets one party convince another party that he knows a secret validating a statement, whilst not revealing the secret.

A zero-knowledge key-statement proof (ZKKSP) is a special type of ZKP where the secret is a private key corresponding to a known public key. The private key satisfies additional constraints, such as hashing to a given value.

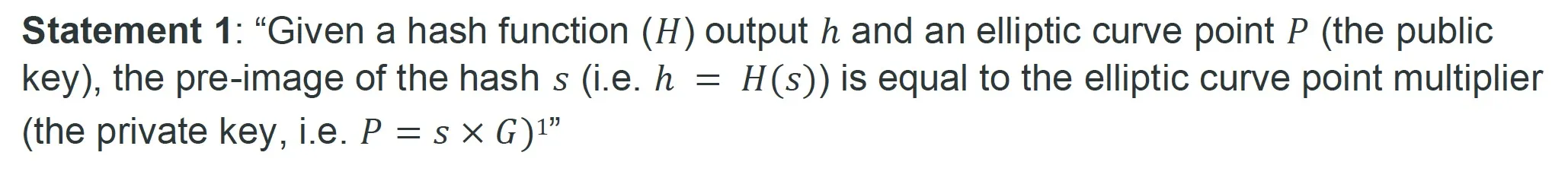
The nChain white paper introduces an efficient approach for ZKKSP. Compared with zero-knowledge proofs for general statements such as zk-SNARKS, ZKKSP enjoys several salient advantages:

1. ZKKSP does not require a trusted setup, an issue that some (e.g. pairing based) zk-SNARKS suffers from.
2. Key-statement proof in zk-SNARKS requires an elliptic curve multiplication circuit, resulting in extremely computationally demanding proof generation and excessively large proof size on the prover side. By contrast, ZKKSP removes the circuit by:

• Working in the same ECDSA elliptic curve than the public key is in
• Checking consistency between the public key and the generated zk-proof; specifically, checking consistency against commitments embedded in the zk-proof¹.

In ZKP, a statement/computation is usually encoded in an arithmetic circuit, consisting of addition and multiplication gates. As Figure 1 shows, zk-SNARKS contains sub-circuits for both a hash function and elliptic curve multiplication. The later circuit checks consistency against the known ECDSA public key. ZKKSP only employs the hash circuit and removes the other circuit, which is at least an order of magnitude larger than the former. Interested readers can refer to the white paper for more details, which we omit here due to space limit.

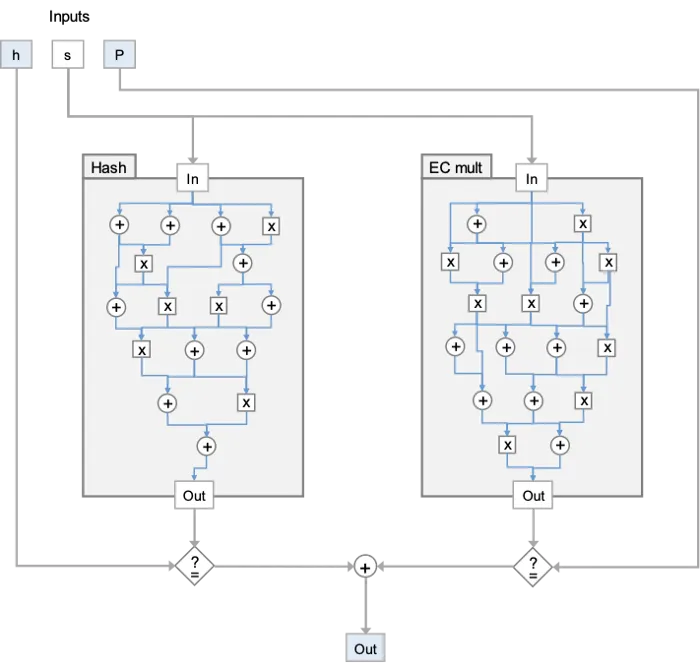
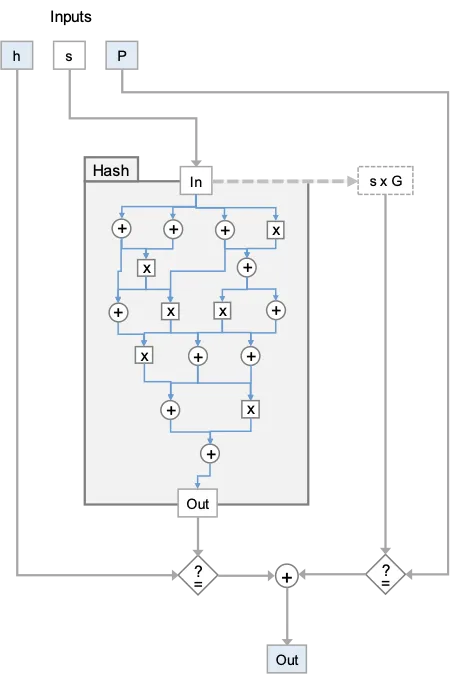
Implementation

We fork an existing library called ZoKrates to generate the arithmetic circuit for SHA256. After modifying the circuit format, we implement the rest of key-statement proof as laid out in the white paper.

ZoKrates

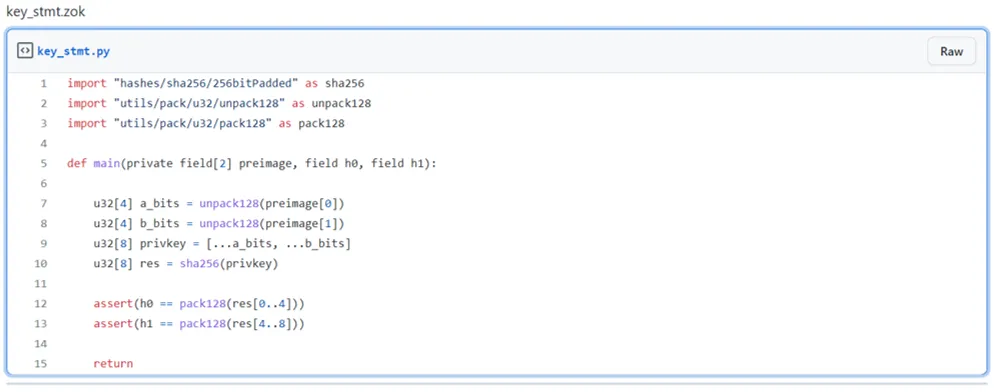
ZoKrates⁴ is a toolbox for zkSNARKs on Ethereum. It consists of a domain-specific language, a compiler, and generators for proofs and verification smart contracts. Below is a source program written in ZoKrates that checks sha256(preimage) == h⁵.

Workflow

The prover runs the following commands sequentially to generate a proof.

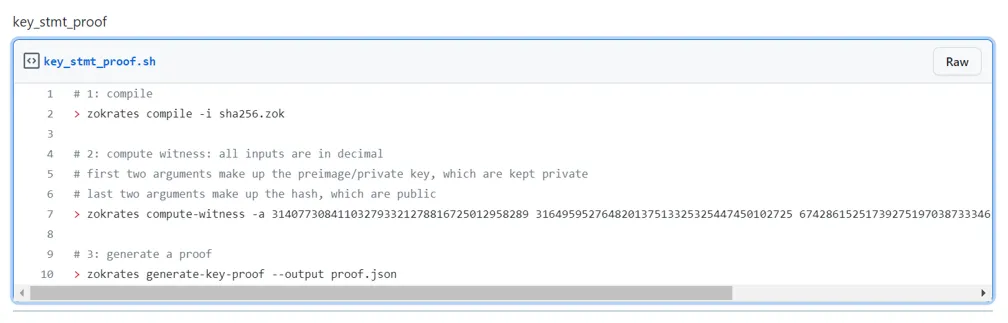
The prover sends the generated proof in proof.json to the verifier. The verifier runs the following command to check if the public key matches the hash value. Note this proof is non-interactive and does not require interaction between the prover and verifier, thanks to the Fiat-Shamir heuristic.

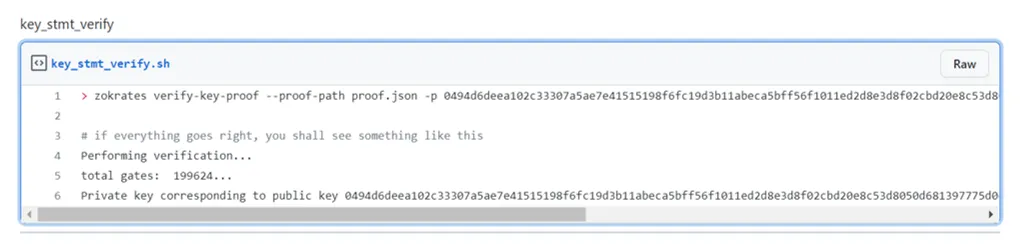
You can find the complete code at our Github.

Application: Outsourced Vanity Address Generation

This section describes applying ZKKSP to outsourcing Bitcoin vanity address generation.

Since searching for a vanity address can be computationally expensive, it is common for the search to be outsourced. Traditionally, either the buyer gets the required value before the seller gets paid, or the seller gets paid before releasing the required value, or they must both trust an escrow service. By employing ZKKSP, the sale of a vanity address can be made trustless.

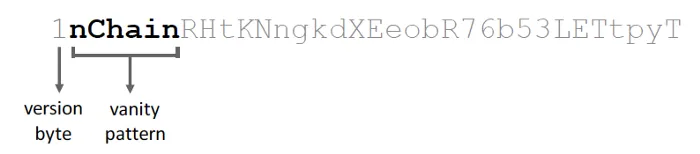
The protocol for this is detailed as follows.

1. The Buyer and Seller agree on the required vanity pattern and the price (in BSV), and establish a communication channel (which does not need to be secure).
2. The buyer generates a secure random secret key sk_B and corresponding elliptic curve public key pk_B = sk_B * G
3. The buyer sends pk_B to the seller.
4. The seller then performs a search for the required pattern in the Base58 encoded address derived from pk = pk_B + i * G by changing i.
5. When an address with the required pattern is found, the seller saves the value , signals to the buyer and sends them pk_S = i * G and the SHA256 hash .
6. The seller also provides a ZKKSP to the buyer that the pre-image to is the private key corresponding to pk_S.
7. The buyer verifies the proof, and also confirms that the address pk = pk_B + pk_S corresponding to matches the agreed pattern. At this point (by virtue of the proof), the buyer knows that learning the value i will enable him derive the full private key for the vanity address (sk_B + i), and that particular value hashes to h = H(i).
8. The buyer then constructs a hash-time-locked contract (HTLC) transaction Tx_1 which contains an output that contains the agreed fee. This output can be unlocked in in two ways:
   i. With a signature from the seller and the hash pre-image, i, at any time.
   ii. With a signature from the buyer after a specified time (OP_CLTV⁶)
9. The buyer then signs and broadcasts this transaction to the blockchain, where it is mined into a block.
10. Once confirmed, the seller can claim the fee in the output of Tx_1 by providing a transaction Tx_2 supplying their signature and the value i to unlock the hash-lock, which is then revealed on the blockchain.
11. The buyer calculates the final vanity address private key sk = sk_B + i, where pk = sk * G
12. If the seller fails to supply the value i before a specified OP_CLTV time, then the buyer can provide their signature to re-claim the fee (to prevent the fee being lost due to an uncooperative buyer).

The exchange is fully atomic and trustless, meaning the buyer only gets paid if he provides a valid secret value 𝑖 which is revealed publicly on the blockchain. Furthermore, the full private key is not known even to the seller, due to the splitting of the private key.

Summary

We have shown how to prove key statement, in which the secret private key hashes to a given value. While primitive at first glance, ZKKSP is extremely powerful to enable many atomic fair exchanges in two general steps:

1. Seller proves to buyer using ZKKSP that he knows a secret the latter needs and it hashes to a given value;
2. The buyer sets up a smart contract that only pays out if the hash preimage is given.

Note step 1 is done off chain and can be computationally intensive, while step 2 is on chain and extremely light weight.

The same technique can be applied to demand the private key satisfies other requirements (i.e., circuits), such as starting or ending with a given pattern.

***

[1] These can be achieved either with a non-succinct proof system for circuit satisfiability or with a discrete-log based SNARK. We have implemented the former.

[2] Internal gates are for illustrative purposes only — the real circuits would have 1000s of gates.

[3] The circuit checks that the output of the hash is equal to the EC public key: the values highlighted in blue are revealed to the verifier, all other values are encrypted.

[4] ZoKrates — Scalable Privacy-Preserving Off-Chain Computations, 2018

[5] Both preimage and h are divided into two parts, since basic type field cannot accommodate 256 bits.

[6] “OP_CLTV” on BSV

Acknowledgements

This is a joint work between nChain Limited and sCrypt Inc.

Watch: CoinGeek New York presentation, Kensei: the Gateway to the Definitive Blockchain

New to blockchain? Check out CoinGeek’s Blockchain for Beginners section, the ultimate resource guide to learn more about blockchain technology.