An election integrity silver bullet

Getting your Trinity Audio player ready...

This post originally appeared on the Unbounded Capital website and we republished with permission from Dave Mullen-Muhr.

The recent U.S. presidential election has reignited a controversy over election integrity. Like many of today’s politically charged topics this conversation has largely resulted in the consolidation of two tribal camps:

• On one side (side X) you have voters concerned about the integrity of elections from the point of view of the eligibility of voters and the accuracy of the tabulation of their votes. 

E.g. How can an election have integrity if voters are unable to trust the accuracy of the tally?

• On the other (side Y) you have voters concerned about the integrity of the election from the point of view of ease of access to citizens seeking to vote and the concern that more onerous voter verification will yield disenfranchisement of eligible voters.

E.g. How can an election have integrity if voters are unable to cast their votes?

Unfortunately for both sides, the current systems largely leave each disappointed and prone to accuse their opposition of foul play (Side X: Voting Machine Supplier Criticized by Trump in Spotlight on Election Integrity; Side Y: Supreme Court Declines Republican Bid To Revive North Carolina Voter ID Law). Take the adoption of technological innovations like electronic voting machines as an example. Computers are an obvious tool to enlist when the task is to count over one hundred million votes. In most other domains the widespread adoption of electronic computational tools would be a no brainer. However, when examined through the context of this election integrity debate it is less clear. Side X is left concerned that electronic voting creates more of a central point of failure that can increase the likelihood of large scale errors (relative to widely distributed hand counting). Side Y is largely concerned about where the electronic voting machines are placed and how simple it is for voters to use them. Does a voter need to leave work on election day and drive 30 mins to a polling location? Why can’t they just vote at home? For this reason mail-in-ballots which are eventually tabulated by machines might sound attractive but this further concerns side X.

In James Carse’s book Finite and Infinite Games he suggests that “finite players play within boundaries, while infinite players play with boundaries.” Rather than getting stuck in the morass of this hot button political debate, is there perhaps a third-way; a solution outside the boundaries that satisfies both sides of the election integrity debate? If such a solution exists it would need to satisfy two key features: 

• Ensure integrity of voter eligibility and tabulation
• Maximally reduce the friction for eligible voters to cast votes

Hashes

Key to Bitcoin’s design is the cryptographic data structure called a Merkle tree. Merkle trees are an elegant solution that can potentially benefit both sides of the election integrity debate without adding any additional concern to either camp. So what is a Merkle tree? To answer that we first need a brief explainer of cryptographic “hashes”. A hash is sometimes described as a digital fingerprint. Why? Because each piece of digital data has a unique hash when transformed through a hashing algorithm, much like how each human has a unique fingerprint. The value of a hash is similar to the value of a fingerprint in that both draw from an extremely diverse and complex sample (for hashes: all digital data; for fingerprints: all humans) and create a unique identifier in a standardized form. For fingerprints this standardized form looks like this: 

 

For hashes (we will focus specifically on the hashing algorithm SHA-256) this standardized form looks like this:

aa5a762c4bf21db24785e7be5d3a85005e6043c0ea84a07f91c085e9d7026909

The above human fingerprint is unique from any other, but with the naked, untrained eye it looks the same as all its counterparts: same shape, same size, same general curvy lines. Similarly, the hash of another piece of data will be completely unique but it will have similar features: same length (64 characters), same sample of numbers (0-9), and same sample of letters (a-f). 

The utility of this fingerprint and its digital fingerprint (hash) counterpart is that if one locates the human who created the above fingerprint they can confirm he was the same individual who initially created it. Similarly, if one locates the data that was hashed to create the “aa5a7…” output, they can confirm it is the exact same data which was initially hashed.

One last key characteristic of hashes illustrates their superiority to fingerprints which will become clear later on when applied to the voting integrity exercise: any change to the originally hashed data, no matter how minute, will yield a completely different output. While fingerprints rely on humans or computers to visually inspect characteristics of the print and compare them to others in order to find a match, hashes can be automated since each hash is completely distinct. Take for example the hash used above: 

aa5a762c4bf21db24785e7be5d3a85005e6043c0ea84a07f91c085e9d7026909 

This is the output returned when you hash the text: “Unbounded Capital” (with no quotation marks, capital U, and capital C). Try it for yourself here, here, here or anywhere else that you can calculate a SHA-256 hash. But what happens if we add a period at the end and input: “Unbounded Capital.”? That outputs the following hash: 

14af1c9c5cb4ed6bfb1155a3eff78d14b35a2589e1f2f0d9a42ddf3f30e34ab2

Despite the relatively inconsequential change to the text (data) input into the hashing algorithm, the output hash value is totally different. This is unlike fingerprints where a minor change to a finger only slightly changes the visual representation in the fingerprint which can cause confusion when trying to compare it across a sample. This superior feature of hashes lends itself to automation since it’s much easier for a computer to search a database for standardized text than it is to search for a fundamentally similar, but slightly inconsistent image.

Merkle trees

Now that we understand hashes we can understand the Merkle tree, which is a cryptographic data structure that depends on them. A Merkle tree is a hierarchical series of hashes. 

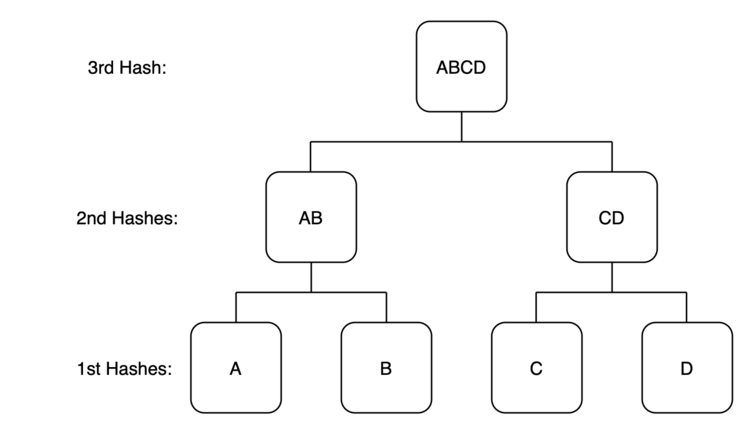
Imagine we have four pieces of data: A, B, C, D. Each piece of data can be hashed independently to yield their own unique digital fingerprint (hash A, hash B, hash C, hash D). Next, we can take these individual hashes and create pairs of two which are hashed together (hash AB, hash CD). At this point (labeled “2nd Hashes” in the diagram), we now have two hash values which each contain two other hash values. Finally, if we hash these last two values together we now have one single hash value (hash ABCD) that contains the hashes of all underlying hashes. Because of this structure, the final hash (labeled “3rd hash”) acts as a group digital fingerprint which verifies the integrity of all the original data in A, B, C, and D.

Let’s think through the value of this structure. The value of hashing A is that if any change is made to the data contained in A it will be easily identifiable: it will yield an entirely different digital fingerprint. Because the hash of A is included in the hash of AB, any change to the data in A is not only noticed at the level of A, it is also noticed at the level of AB. Continuing the domino effect:

• The change to the data in A causes a change to the hash of A
• This change results in a change to the data in AB which causes a change to the hash of AB
• This change results in a change to the data in ABCD which causes a change to the hash of ABCD.

The end result of organizing and hashing the data in the Merkle tree is that any change to any of the raw data is immediately and irrefutably reflected in the single hash at the top of the tree. In other words, to ensure the integrity of the underlying data, all one needs to do is monitor the top hash, or the “Merkle root”. If the Merkle root is accurate, there is effectively 100% certainty that the underlying data has not been altered.

Simple vote verification

Another key feature of the Merkle tree is the ability to easily prove to someone that their unaltered data was included in the cumulative set of data. Let’s explicitly think about these Merkle trees in the context of election integrity. If A, B, C, and D are individual’s votes then the voters who cast them might want to be reassured that their vote was counted in the final tally (satisfying side X’s concerns). For voter A to do this, they would only need to be provided a few pieces of data: the hash of B, the hash of CD, and the Merkle root (hash of ABCD). 

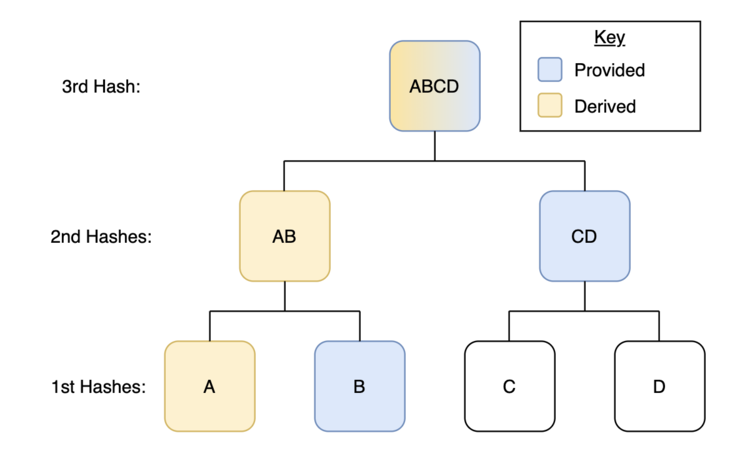
Let’s think through why this is the case. If voter A has their vote or some type of vote receipt in digital form, they are able to hash it themselves (just like we hashed “Unbounded Capital”). If they are provided the hash to B (I won’t explain this in depth here, but another benefit of hashes is that they are “one-way-functions” meaning if the hash of B was shared with voter A, voter B would still maintain their privacy. E.g. voter A cannot determine voter B’s name, vote, or other private information via receiving the hash of vote B) they can then combine their derived hash of A with the hash of B to derive the hash of AB. If they are then provided the hash of CD they can combine it with their derived hash of AB to derive ABCD. If the election’s Merkle root was posted publicly, all that voter A would need to do is compare this hash against the official election Merkle root. If they match, they know with 100% certainty that their vote was tallied. If they do not then they know something is illegitimate.

Verifiable electronic voting

Verifiable electronic voting using Merkle trees could be the foundation of a silver bullet that remedies the complaints of both sides X and Y in our ongoing election integrity debate. Imagine a voting paradigm where voters could vote online in a matter of minutes from the comfort of their home (satisfies side Y) ALL WHILE having the certainty that their vote was included in the final tally (satisfies side X).

The above example of manually tracing one’s vote through a Merkle tree might sound unreasonably complicated. Is your grandma going to hash her vote all the way up a 150 million data point Merkle tree to compare it against the election Merkle root? No offense to your grandma, but absolutely not. However, this complexity could easily be hidden in the background. In fact, when your grandma is using the internet today she is routinely hashing information, sending those hashes, receiving hashes, comparing hashes against hashes. It is all happening in the background of her browser as she downloads recipes and emails her friends. An election paradigm that ensures the integrity of the votes cast AND reduces the friction of casting the vote need not ever mention the words “hash” or “Merkle”. Instead, voters would simply log into normal looking mobile applications or view the results on web browsers. However, what would appear on the voter’s screen in a user friendly way to say “Your vote was counted!” would be calculating information based on publicly available data and confirmed via the mathematics of cryptographic hashing algorithms.

A verifiable electronic voting paradigm would also provide another key piece of currently disputed information with near 100% integrity: the number of votes that were cast. These are only a few ways that a new cryptographically informed voting paradigm could improve election integrity for everyone regardless of any tribal political affiliations. The development of other foundational tools which could plug into this voting mechanism, namely verifiable online identity, could even further improve an upgraded voting experience and ensure that every eligible voter (and no one else) was given the ability to cast their vote, for example. These are features which would require innovation beyond merely organizing the data in a Merkle tree, but they are foundational technologies being built on Bitcoin (BSV) today. 

In short, nothing about this vision is unattainable. The necessary puzzle pieces that would be required to create incredibly high-integrity online voting systems are either already developed or in development today. Despite sounding complex, the Merkle tree data structure is something that can be done trivially by computers. In fact, it is already constantly being done with Bitcoin. Today, each Bitcoin transaction is organized into this structure (even when there are millions of transactions over a small period of time) which is part of why Bitcoin is seen as such a trustworthy accounting system with an effectively unalterable history of transactions. Bitcoin also provides the neutral and public data layer where this voter data could reside, resilient to the single point-of-failure concerns of private voting systems and databases. The ability to process ~150 million votes in a single day, while taxing for many less trustworthy (and private) systems, is simple for Bitcoin today. This processing ability will only improve over time. Bitcoin is currently on track to make processing 150 million votes over a short period of time a miniscule drop-in-the-bucket relative to its total processing power, which aims to facilitate millions and billions of transactions per second in the near future. The same level of efficiency, however, cannot be said for popular networks like BTC (the popular version of Bitcoin) or Ethereum which would be unable to process this quantity of transactions in any reasonable timeframe.

To learn more about the Bitcoin blockchain and relevant projects currently being built on it which might one day be used to enable this type of voting paradigm visit the following links:

• Unbounded Capital’s Free E-Book explaining BSV and comparing it to popular alternatives like BTC and Ethereum
• Twitter thread introducing the B-Vote voting platform on Bitcoin
• Article on Bitcoin Identity Solution “Legally Chained”