Zero-overhead private timestamping in Bitcoin

Getting your Trinity Audio player ready...

This post was first published on Medium.

Bitcoin has many potential uses far beyond payments. Each block has a timestamp that is cryptographically secured. By recording data in a transaction and thus a block, it can be proven to any external auditor that the data has not been tampered with since a particular date. Timestamping can be particularly useful for time-sensitive data: patents, insurance claims, invoices, notary, etc.

This is usually done with OP_RETURN. We introduce a novel alternative to using Bitcoin as a timestamping server, that is both private and with no overhead.

ECDSA Signing

In ECDSA, a random number k, called nonce, is chosen when signing. G is the generator point.

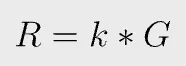
r is the x coordinate of R.

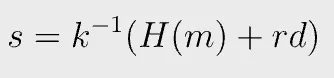
H() is a hash function, m is the message being signed, and d is the private key.

The signature is the pair (r, s) and is made public on the blockchain. Both k and d must be kept confidential.

Embed Data in k

Since k can be any random number, we can embed data in it as follows:

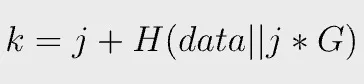
j is another number chosen randomly as k before. The new k is just a nonce as before and can be used to sign a message, which is verified in the same way.

r, and thus R¹, is exposed on the blockchain as part of a signature. To prove data is embedded in it, the prover has to disclose both J and data as below:

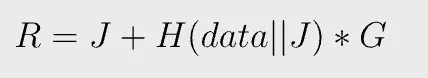
Anyone can verify R is created with knowledge of data by verifying if Equation 4 holds, since all variables (R, J, data, G) are publicly known. Note that J appears twice and once inside a hash function. It is not possible to solve for it, given R after the fact. Thus R on the blockchain commits to data.

Private

If Alice has some data to timestamp, she can spend one of her own coins and create k using Equation 3. An outside observer can only see r in her signature and cannot know if it is from a k generated with or without Equation 3. The timestamping transaction looks the same as a normal payment transaction, making it ultimately private.

No overhead

If Alice does not have any bitcoin, she can ask Bob to timestamp her data into his signature. If Bob has to sign to spend coins anyway, the timestamping comes at no overhead to him. Bob can be a timestamping service and charge a fee for doing so. He gives back Alice only J, without disclosing k. Alice uses Equation 4 to verify her data is indeed committed in r on the blockchain.

What goes into data

Usually, only the hash of the raw data needs to be committed. The data can also be the root of a Merkle tree.

Acknowledgements

The idea comes from this MIT lecture, in the context of Schnorr signatures, versus ECDSA signatures here.

[1] Strictly speaking, there are two corresponding points/Rs, given a r on an elliptic curve. We can verify if any of them makes Equation 4 holds.

Watch: CoinGeek New York presentation, Smart Contracts & Computation on Bitcoin