This post was first published on Medium.
We have empirically demonstrated that any Turing machine can be simulated on Bitcoin and thus definitively proven it is Turing-complete. We have implemented a Turing machine that recognizes balanced parentheses and deployed it on the Bitcoin blockchain. Any other Turing machines can be simulated in the same way.
Introduction to Turing machine
A Turing machine consists of the following components (simplified):
- A current state, out of a limited set of states (with one state marked as initial state, some states as accepted states)
- A tape with storage cells and a read/write-head that can move on the tape
- A so-called transition function that tells the machine what to do and when.
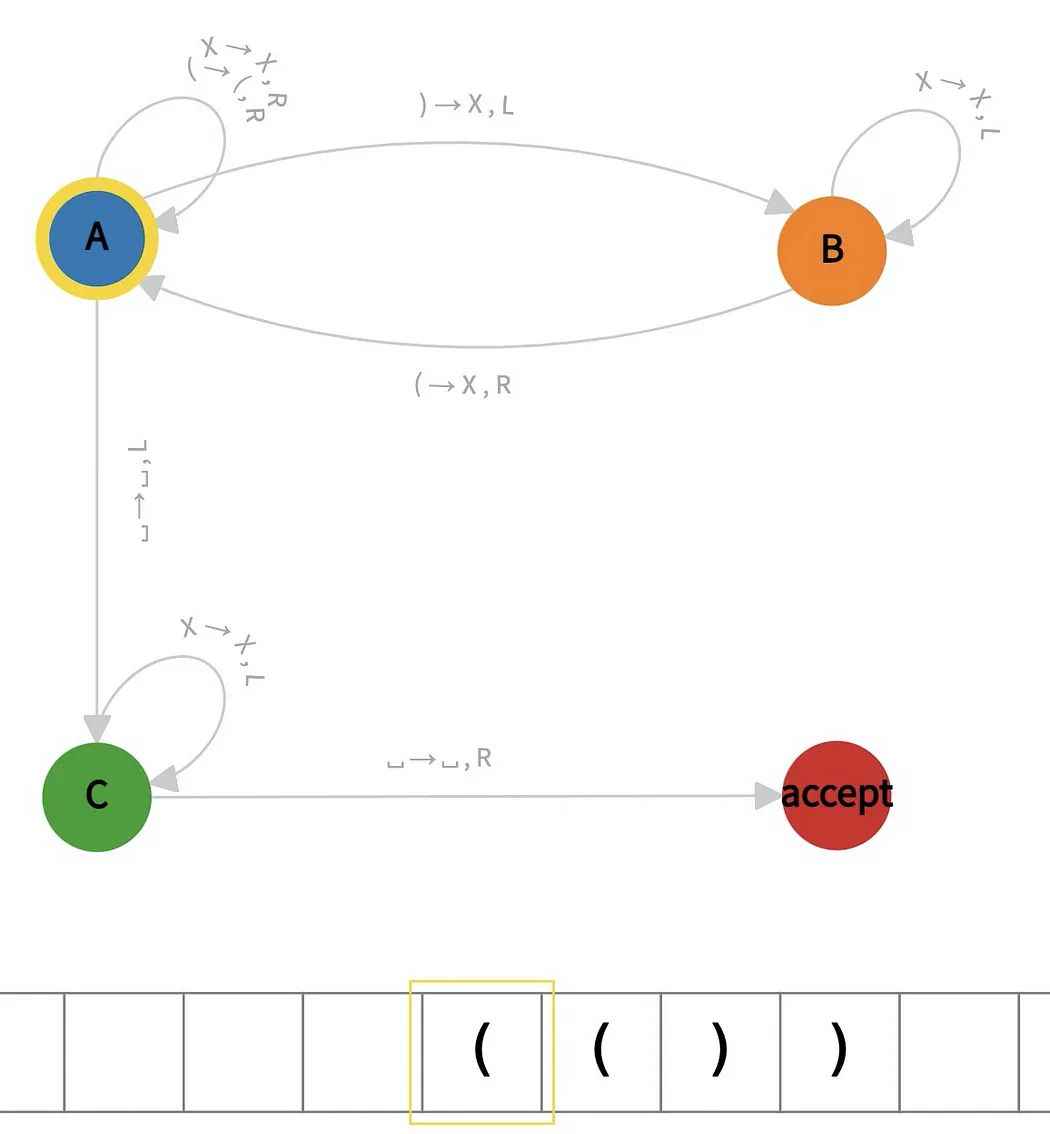
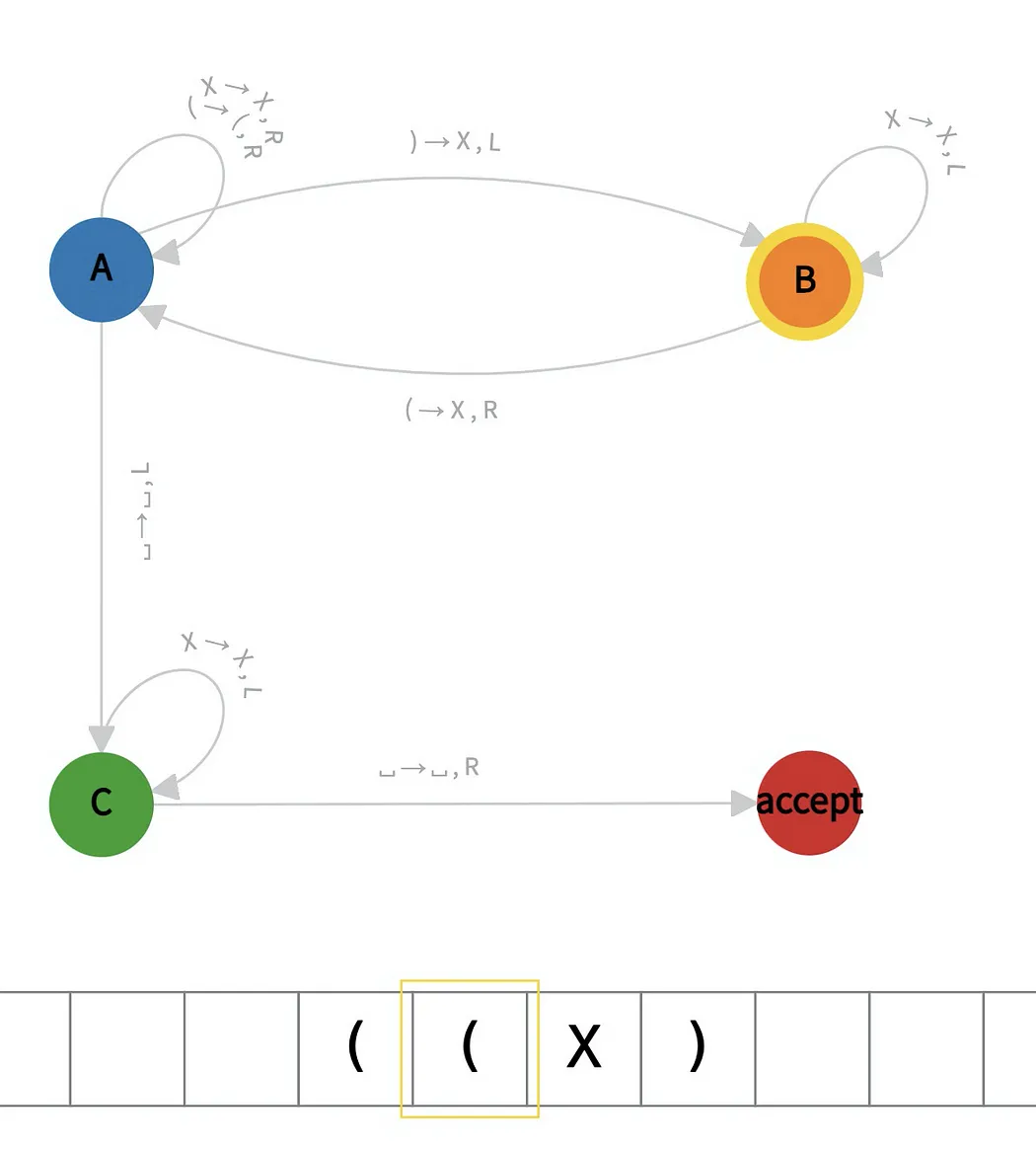
In the example below, we show a Turing machine for checking balanced parentheses. Its initial state is A, and it contains one accepted state. The transition function says, for instance, if the machine is at state A and its head reads symbol “),” it should write “X” in that cell and move left, transitioning to state B.
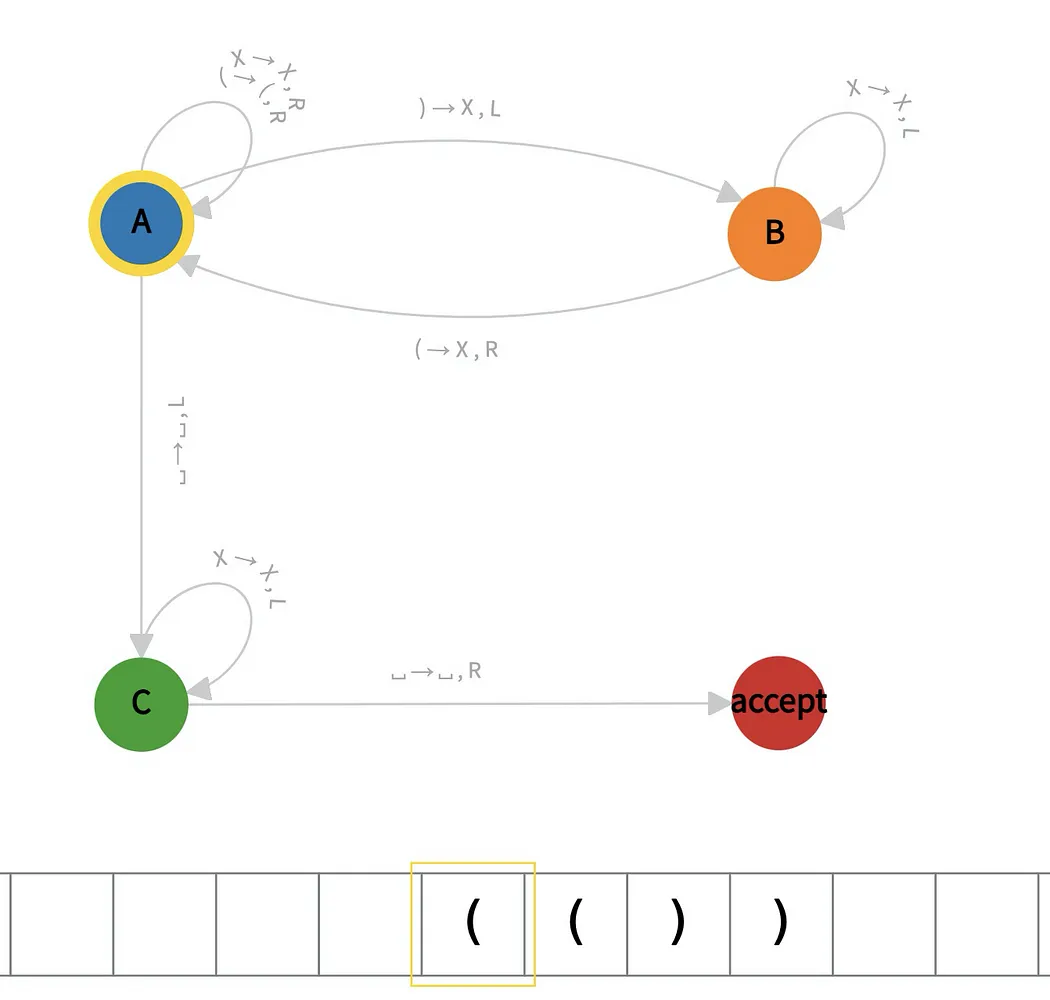
Church-Turing Thesis
The Church-Turing Thesis states that the Turing machine can compute anything that can be computed. It is the very definition of computation and the fundamental tool for reasoning about computers.
Simulate Turing machines on Bitcoin
We show a generic way to simulate Turing machines on Bitcoin. We take snapshots of a running Turing machine: head position, current state, and tape. Snapshots are stored in a stateful Bitcoin smart contract. More specifically, they are in the outputs of Bitcoin transactions. Each step in running the Turing machine is triggered by a Bitcoin transaction. The Turing machines can keep running unless it enters an accepted state.
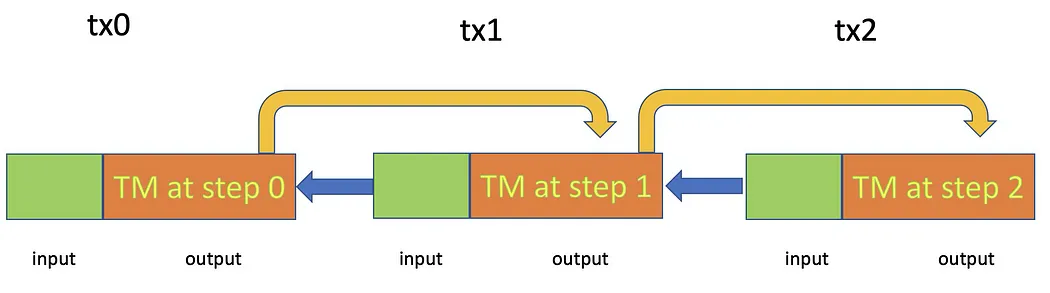
Implementation
To demonstrate the feasibility of simulating Turing machines on Bitcoin, we have implemented the aforementioned Turing machine to check balanced parentheses, as shown below.
A Turing Machine contract checking balanced parentheses
Each time the public function transit() is called in a transaction, the machine advances one step.
- Line 3–6: define states, including initial state and accepted state
- L9–12: define all symbols
- L19-30: define the transition function as a table
- L37: read the symbol from head
- L40–43: use the current state and head symbol; we look up in the transition function table to find the new state (L46), write to the tape (L48), and move the head (L50).
- L51–59: initially, the tape contains only the input string, such as “(())()().” If any time the tape runs out, either on the left (L52) or right (L56), a blanked cell is added. This ensures the tape can be arbitrarily long and is unbounded (but not infinite²).
Deployment
We have deployed the Turing machine above to Bitcoin and run it on the input string “(())()().” The complete execution is shown below.
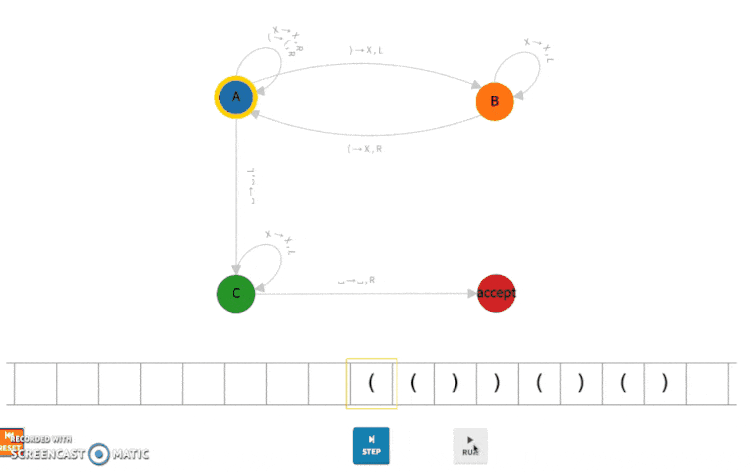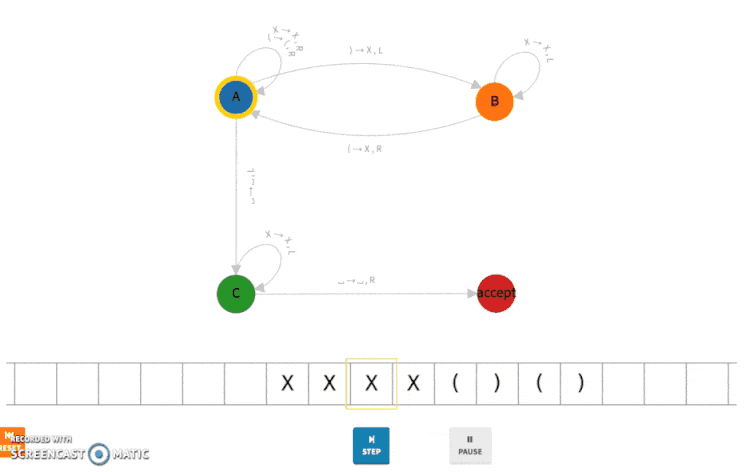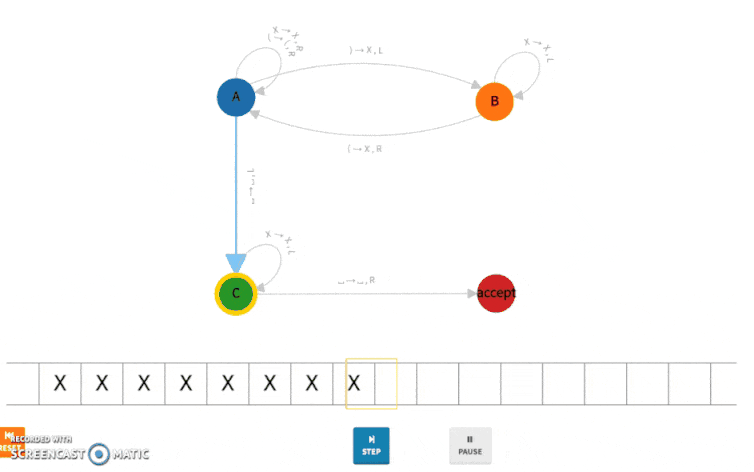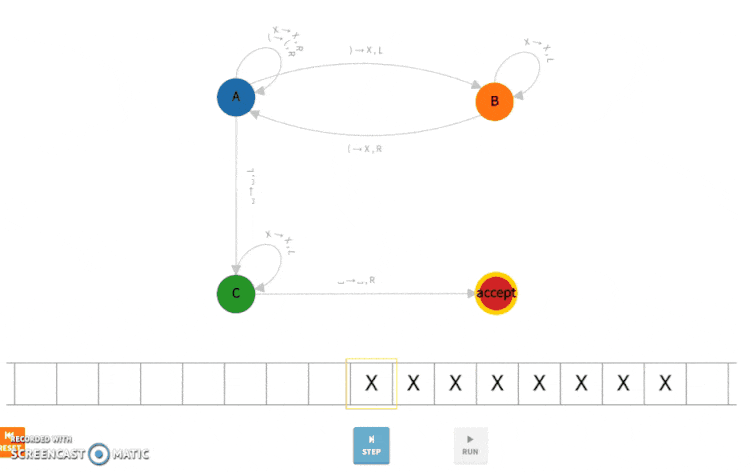
This is Turing Machine at step 0:
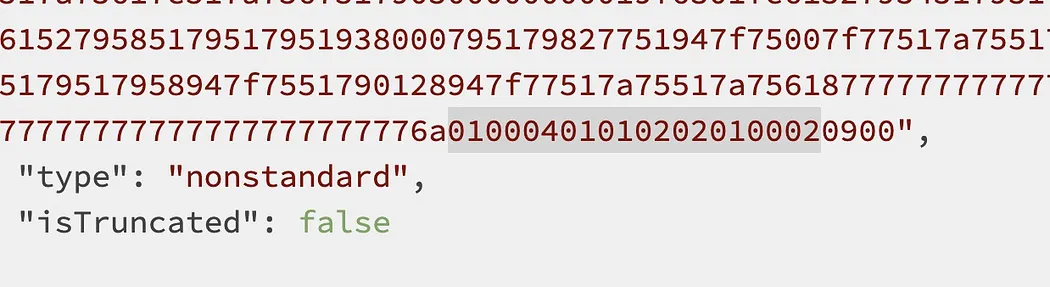
You can see the snapshot of the Turing machine is encoded in this transaction.
Similarly, this is step 3:
And it is encoded as follows:
Turing Complete Proof
It is straightforward to adapt the Turing machine contract above to implement any other Turing machines by simply changing the states, the symbols, and the transition function. Thus, any Turing machine can be simulated on Bitcoin, conclusively proving Bitcoin is Turing-Complete by definition. QED.
In computability theory, a system of data manipulation rules is said to be Turing-complete if it can be used to simulate any Turing machine.
Update: 12/2022
There is an independent paper proving a UTXO-based blockchain is Turing Complete using logic similar to ours: Self-reproducing Coins as Universal Turing Machine.
Update: 2/2023
Another independent paper proves Bitcoin is Turing Complete by simulating any counter machine: Computationally sound Bitcoin tokens. It requires changing the Bitcoin script to include covenants, which is actually not needed because of OP_PUSH_TX.
Acknowledgements
Thanks goes to Pasquale Valentin for helping with the deployment of the contract on Bitcoin.
***
[1] We have previously shown Bitcoin is Turing-complete by implementing Turing-complete systems on it, such as Conway’s Game of Life and Rule 110.
[2] Infinite and Unbounded By Craig Wright | 14 Sep 2021
Watch: Smart Contracts and Computation on BSV
New to blockchain? Check out CoinGeek’s Blockchain for Beginners section, the ultimate resource guide to learn more about blockchain technology.
