This post was first published on Medium.
In general, to compute the hash of an input (called preimage), its entirety is needed. We show a novel technique to compute the hash with only part of the preimage, for a wide range of hashing algorithms.
How SHA256 Works
Let us look at SHA256 as an example. Internally, it works as follows:
- The preimage is split into chunks of 512 bits. Padding is appended if necessary.
- Each chunk is iteratively fed into a function g, together with an internal state (current hash h0-h3), whose output is used as input to the next iteration.
- The last state is the final hash.
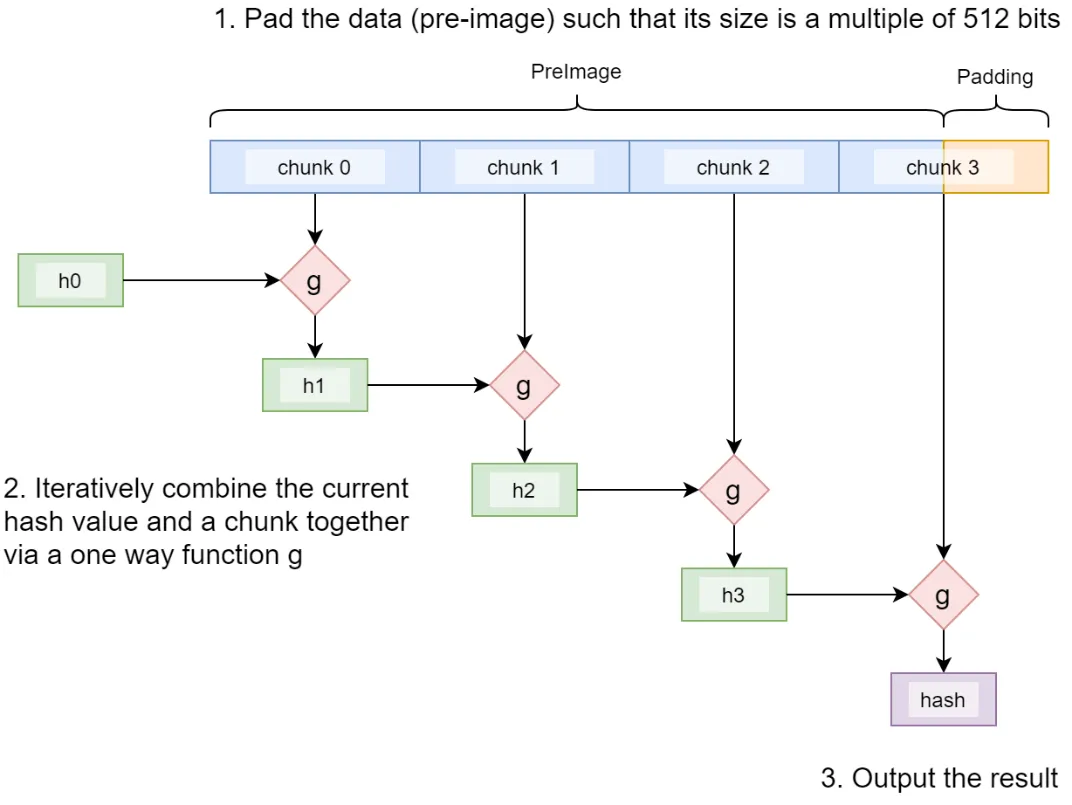
This process is called the Merkle–Damgård construction. g is a compression function that takes two fixed-lengths inputs and produces a fixed-length output.
The Partial Preimage Technique
Due to the iterative nature of the construction, we can obtain the same hash if we start from any intermediate iteration, as long as we have the current internal state/hash and the remaining preimage.
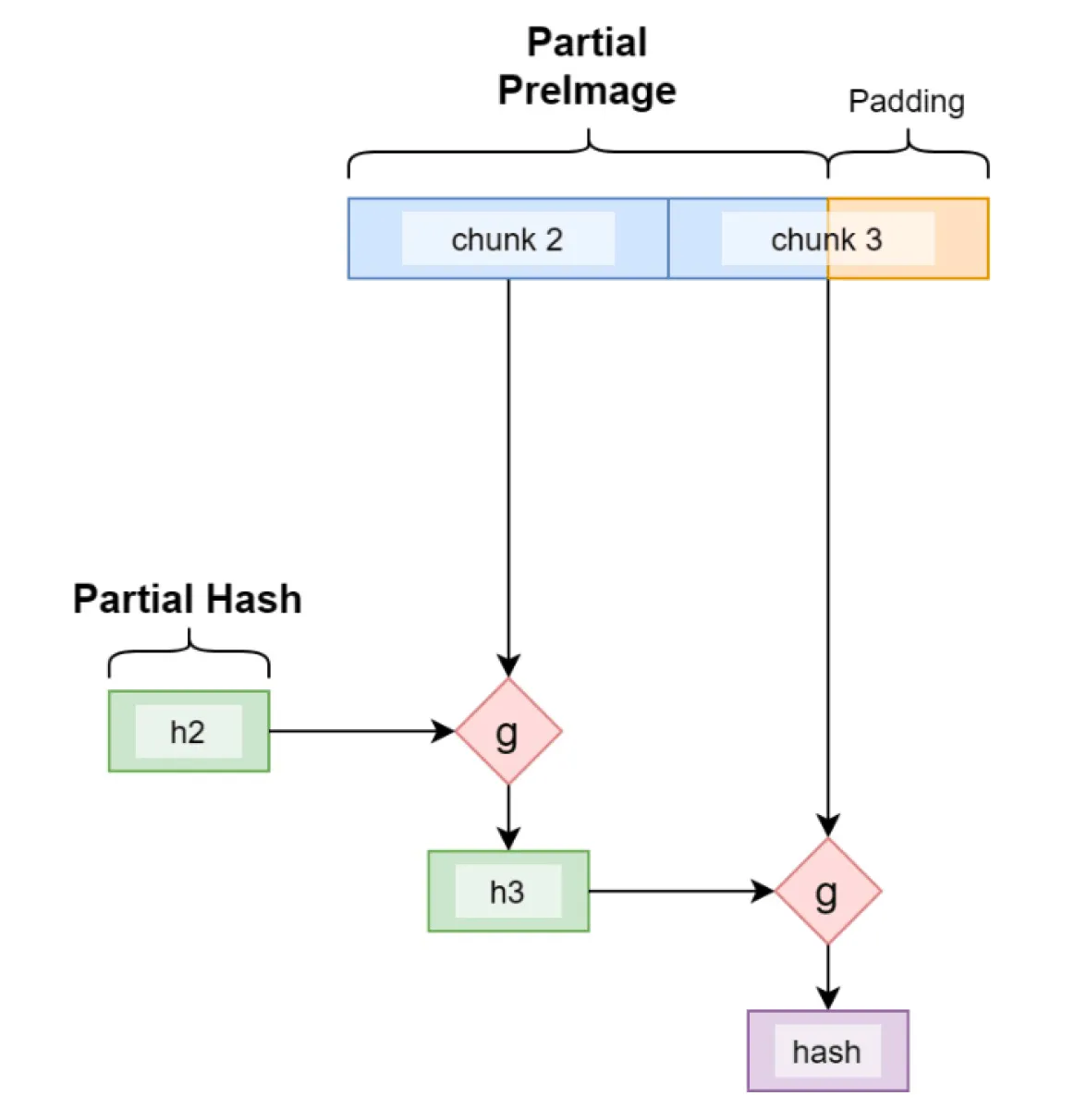
Length Extension Attack
The iterative and stateful nature of SHA256 makes it vulnerable to the so-called length extension attack. An attacker can use SHA256(message1) and the length of message1 to calculate SHA256(message1 ‖ padding ‖ message2)¹ for an attacker-controlled message2, without needing to know the content of message1.
We turn the attack surface on its head and use it to our advantage.
Example Usage: Fetch a Parent Tx’s nLocktime Without the Full Tx
We use a toy example to demonstrate how to leverage the aforementioned technique. The contract requires that the spending transaction that unlocks it must add a specified delay to the locktime. This usually requires injecting the full parent transaction and parse it to get the locktime. Thanks to the technique, we can achieve it by only including the last chunk².
Function partialSha256() implements SHA256 and computes the sha256 hash of a transaction from a trailing part of it and the current hash for all the preceding parts (h0-h7). Line 53–158 correspond to applying function g to one chunk.
Discussion
It may not make sense to apply the partial preimage technique to the above contract, since the overhead of implementing SHA256 outweighs the saving of injecting only a partial transaction. However, the benefit can outweigh the overhead when the transaction is large, which is becoming more and more often as script and transaction size continue to grow.
Besides SHA256, this technique also applies to hashing algorithms MD5, RIPEMD-160, SHA-1, and other SHA-2 that are also based on the Merkle–Damgård construction. Given the prevalence of these hashing algorithms in Bitcoin, the technique can find wide usage.
Acknowledgements
Both the idea and code of partial preimage go to Ying Chan, formerly at nChain and now at Cambridge Cryptographic.
***
NOTES:
[1] ‖ is concatenation.
[2] Assume the 4-byte nlocktime is in the last chunk, not split across the last 2 chunks.
Watch: CoinGeek New York presentation, How to Achieve Green Bitcoin: Energy Consumption & Environmental Sustainability
New to blockchain? Check out CoinGeek’s Blockchain for Beginners section, the ultimate resource guide to learn more about blockchain technology.
