Proof of Work in Bitcoin: No floating point number used

Getting your Trinity Audio player ready...

This post was first published on Medium.

We elaborate how Proof of Work (PoW) works in Bitcoin.

Proof of Work

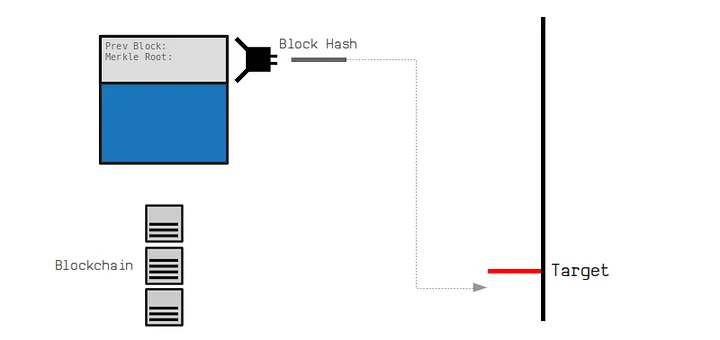
The core of the PoW (Proof of Work) process involves finding a hash below a target value set by the network. The hash function used by Bitcoin is double SHA-256, which produces a 256-bit hash value. Miners generate hash values by combining the block header information with the nonce and passing it through the hash function. Since the output of the hash function is unpredictable, miners essentially guess different nonce values until they find one that produces a hash below the target value. This process requires a significant amount of computational power and is referred to as mining.

Target vs difficulty

The target is a 256-bit integer that all Bitcoin miners are aiming to find a hash value below. Valid blocks must have a hash below this target. 256-bit means it’s extremely large and can represent a vast range of values. This granularity allows for precise adjustments to the network’s mining difficulty.

Difficulty is a measure of how difficult it is to find a hash below a given target. The Bitcoin network has a global block difficulty.

The target inversely relates to the mining difficulty. A lower target means higher difficulty, as there are fewer possible hash values that meet the criteria. Conversely, a higher target increases the range of hash values considered valid, reducing the difficulty.

Difficulty adjustment

The difficulty of the Proof of Work puzzle adjusts approximately every two weeks to maintain a constant block time of about 10 minutes, regardless of the amount of computational power in the network.

Every 2016 blocks, the Bitcoin network calculates the time it took to mine the last 2016 blocks. It then compares this time against the desired timeframe of 20,160 minutes (2016 blocks * 10 minutes per block). If the actual time is less than the desired time, it means blocks are being mined too quickly, and the target lowers (increasing difficulty). Conversely, if the actual time is more, indicating blocks are mined too slowly, the target raises (decreasing difficulty).

How is target implemented?

In the Bitcoin block header, a compact 32-bit form is stored (known as “Bits”), not the full 256-bit target. It saves spaces and makes it easier to work with and transmit across the network.

Converting Bits to target

Bits is just a shorthand/compact version of the target. It works like scientific notation, except that it uses base-256 instead of base-10.

It’s basically split in to two parts:

1. Exponent: This gives you the size of the target in bytes.
2. Mantissa: This gives you the initial 3 bytes of the target.

For example, if Bits is equal to 0x1810696F4, you would calculate the target like this:

0x18 in hex is 24.

Leading zeros

In the white paper, “leading zeros” is used as a way to intuitively understand finding a valid hash below the target threshold.

In code, however, the actual criterion for a valid block hash is that it must not exceed a specific target value. Counting leading zeros is thus only an approximation, since hashing to a number of leading zero bits is only a necessary, but not a sufficient, condition for a block hash to be valid.

Function CheckBlock

To see why, consider the target above is shown as full 32 bytes (512 bit) in hexadecimal format below, with preceding zeros.

Target: 0x00000000000000000696f4000000000000000000000000000000000000000000

The following hypothetical block hash is not valid, which only differs from the target in the last byte (0x01 vs 0x00). Even though it has the same number of leading zeros as the target, it is larger and thus invalid.

Block hash: 0x00000000000000000696f4000000000000000000000000000000000000000001

No floating point numbers

A floating-point number is a way to represent real numbers in computing that can accommodate a very wide range of values. The “floating-point” term comes from the fact that the decimal point can “float”; that is, it can be placed anywhere relative to the significant digits of the number. Examples of floats are 0.1243 and 12.245.

In consensus-critical components of Bitcoin, such as adjusting the difficulty or comparing hash values, floating-point representations are avoided because they can behave inconsistently across various computing architectures. This inconsistency arises from potential rounding differences inherent in floating-point arithmetic, which can lead to non-deterministic outcomes. Since the consensus rules of Bitcoin demand complete determinism to ensure all participants agree on the state of the blockchain, the system relies on data types and operations that yield the same result on any machine, thereby excluding floating-point numbers due to their precision loss and rounding errors. Instead, integers are used.

In COPA v. Wright trial, COPA’s witness Adam Back claims the Bitcoin code uses floating point in PoW. This is demonstrably false. All numbers in PoW, target and Bits, are represented as integers. No floating-point arithmetic is used. It is worth noting that difficulty does not show up in code. It is a derived measure from target.

Watch: Why Proof of Work is the most secure model of consensus