Is Bitcoin’s Merkle tree a binary search tree?

Getting your Trinity Audio player ready...

This post originally appeared on ZeMing M. Gao’s website, and we republished with permission from the author. Read the full piece here.

Is Bitcoin’s Merkle tree a binary search tree?

Dr. Craig Wright says Bitcoin’s Merkle tree is a binary search tree. BTC devs disagree and question his qualifications. The questioning by BTC and Dr. Wright’s answers show a typical example of Dr. Wright talking about it at a level and depth that others haven’t thought of.

Ironically, some even question Dr. Wright’s understanding of technology at the undergraduate level, not in spite of this but because of this.

(And it is this same kind of ongoing questioning during the last eight years that dominated the Wright Satoshi subject. Frankly, it is shameful and unjust. It is also what often compels me to explain to others.)

Anyone who might have had an impression that Dr. Wright doesn’t even know the basic stuff should reexamine their basic mindset.

No one should trust what another person says blindly, but a much more common mistake people make about Dr. Wright is to reject him presumptively. It’s time to learn from what has happened again and again. Judging from past repetitive experiences, the basic sense of prudence would require one to think more deliberately and deeply about what Dr. Wright says to just avoid embarrassment.

If you truly wish to investigate the truth in Bitcoin, resist the temptation of focusing on insulated technicalities too much. It is a system. A system that exists in a computational, economic, and legal environment, to be more particular.

Your understanding of these matters highly depends on whether you want a techno-political system that is primarily for censorship resistance or an economic system that is primarily for productivity. Each view can have its own respectful rationales, but one must understand the difference before concluding that others don’t know a thing.

I understand both views very well. I just happen to prefer the scalable and productive economic system to a techno-political law-resistance system. The real world may have room to allow both systems to exist. My preference has to do with the values I believe in, and I understand others have their own values and beliefs.

So please hear me out on this particular question of Bitcoin’s binary search tree. I discuss it not only because it is of unique technical significance but also because it’s a good example to show why one should pay attention to what Dr. Wright says.

Merkle tree and binary tree

Dr. Wright said the Merkle tree structure that was designed by Satoshi originally and has now been implemented in BSV along with SPV (Simplified Payment Verification) which is a binary search tree.

His opponents suggest that it is ridiculously wrong because everyone who has a basic understanding of computer science would know that a Merkle tree is not a binary search tree.

His opponent is right in the sense that the Merkle tree, in its base application taught in school, is not a binary search tree.

But what they do not know is that Satoshi had designed the Bitcoin Merkle tree in such a way that, although it is a Merkle tree, it is also a search tree, even a binary search tree.

Dr. Wright is just unbelievably right, once again.

Let me explain the technical details below.

First of all, the key concept about a ‘binary tree’ refers to a feature that cuts the tree (together a corpus of data) in two halves (hence ‘binary’) in every step. It determines the direction to proceed for the next step based on a match or mismatch and discards the half in the other direction. This is repeated until the target item is located. This binary fashion makes the process very fast and scalable. Because every step is a binary, it progresses exponentially, resulting in a logarithmic scalability.

The fact that half of the data can be instantly disregarded with no risk of losing the target is what creates this remarkable effect. But this necessarily requires that the nodes and leaves in the tree are ordered and balanced in a particular way.

Therefore, calling a tree “binary” means that the tree is constructed in a way that an act (e.g., a search) can be performed in a binary fashion. If the structure does not have this binary feature, then calling it binary would be incorrect. But if the structure does have this binary feature, but no one else knows such a structure and has never called it binary, the one who first calls it would be not only correct but also innovative.

The binary tree can be structured to perform various functions and achieve various goals. When the tree is structured to perform a binary search, it is a binary search tree. But binary trees can be used for other purposes, such as for ensuring data integrity.

So the question is, why does Dr. Wright call Bitcoin’s Merkle tree a binary search tree?

First, if Bitcoin’s Merkle tree is structured in a way to find the location of a certain piece of data and confirm its existence, it is a search tree. This is plain, regardless of what others say.

But is it ‘binary’ and hence a binary search tree? That is a more elaborate consideration.

The answer is yes. Bitcoin’s Merkle tree is a binary search tree because the Bitcoin data is deliberately structured as a key-value database, meaning that each item (a transaction or a hash) is associated with (labeled by) a key. The keys are sequential. There are different ways to structure the keys. It depends on the design of the tree structure and the algorithm (see below for an example). Note, here, the word “key” is a standard database technology, like a label of an item, and has nothing to do with cryptography keys.

Because Bitcoin transactions are timestamped according to the order of time each transaction is received, this sequential order is natural. Now, with the sequential keys built in, each corresponding to a timestamped sequential transaction, you have an ordered and balanced tree of hashes of leaves.

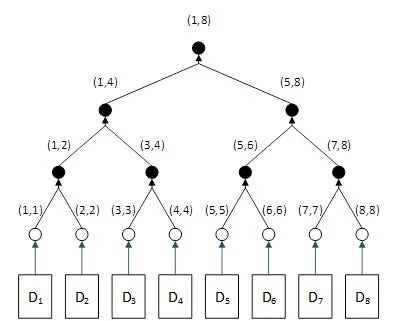
Figure 1 shows an example of such a Merkle tree that is also a binary search tree.

Transactions are denoted by Di. Transaction Di corresponds to hash (i, i), which is a special case of key (i, j) where i=j.

Each node is denoted by a key consisting of a pair of numbers (i, j), such as (1, 4). The meaning of the numbers is quite simple: a node with a key (i, j) means that the data in the node and the child nodes under it cover transactions in the range of i to j. For example, (1, 4) means that the node and the child nodes under it cover transactions 1, 2, 3, and 4. Implicitly, it also means that they are unrelated to transactions 5, 6, 7, and 8, which are covered by the other branch under (5,8).

According to this sequential numbering, (i, k) and (k+1, j) are two neighboring nodes, as indicated by k and k+1. When two neighboring hashes, H (i, k) and H(k+1, j), are concatenated and hashed, it generates a new hash H (i, j). The resulting keys (i, j) are logical because concatenating two neighbor hashes concatenates the two ranges, namely i to k and k+1 to j, to create a new range i to j, hence its resulting hash is denoted as H (i, j). Note that the middle numbers k and k+1 do not appear in the new key (i, j). This is because the range i to j denotes an extended range which necessarily covers the middle numbers k and k+1.

Figure 1 illustrates a simple case where i=1, 2,…8. In reality, i=1, 2,…n, where n is the total number of transactions in the block and can be a large number.

Merkle tree is formed as follows:

1. Hash each transaction Di to get H(i, i). This is the first level of the Merkle tree, in which transaction data items and their hashes have a 1-to-1 correspondence.
2. Hash the concatenation of every pair of neighboring H(i, i) and H(i+1, i+1) to get H(i, i+1). This gets the second level. The second level will have n/2 nodes.
3. Repeat the same process in step 2 above until we reach the final level where only one node remains. This is the Merkle root.

Because the number of nodes in each next level is halved, this process reaches the root (top) quickly. The total number of levels m=log2(n). The more transactions the block has, the greater advantage it enjoys.

For example, when n = 8, m=3. When n= 1 million, m=20; when n=1 billion, m=30; when n=1 trillion, m=40, and so on. You can see that, from n=8 to n=1 billion, the total number of transactions in a block has increased more than 100 million times, and the total number of levels in the tree increases only 10 times.

The above is the basic characteristics of the Merkle tree. But it will be clear that labeling the nodes using sequential keys transforms the Merkle tree into a binary search tree.

In the example shown in Figure 1, suppose we need to search for transaction D5. which corresponds to key (5, 5). We start from the top (root) H(1, 8), which indicates that the block has a total of 8 transactions from 1 to 8).

First, we compare our target (5, 5) with the present node (1,8). Because 5 > 8/2, we know our target is on the right side. We go to the right side to arrive at node H(5, 8) and disregard the entire left branch, which is half of the tree. If this is not obvious in this small example, imagine that if the block has 1 billion transactions, this one step skips 500 million transactions.

Next, we compare our target (5, 5) with the present node (5, 8). Because 5=5, we know we already got this part of the key correct, which is the lower boundary of the transaction range. But because 5<8, we go to the left and reach H(5,5), which corresponds to transaction D5, the exact transaction we are looking for.

Thus, the Merkle tree structured above enables binary search and is thus a binary search tree. There can be no debate over this because it is precisely how a binary search tree is defined.

Such a binary search tree combined with an elaborate design of SPV makes Bitcoin, as implemented in BSV, extremely powerful.

Binary search tree and SPV

SPV itself is another subject matter. Although it has been disclosed in the Bitcoin white paper, SPV has only been properly understood and further developed on Bitcoin SV (BSV). I will skip an explanation of SPV itself, but would like to emphasize it’s relevant to Bitcoin’s binary search tree.

SPV is about scalability. If you only look at an individual incidence of how SPV works with a user submission of the Merkle path of his transaction, it would seem that it has nothing to do with search because the user readily produces the Merkle path, which specifically locates not only the transaction ID but also its location, leaving nothing else to be searched on the blockchain. The only thing that remains is that the recipient needs to compute a Merkle proof to verify the existence of the transaction using the Merkle path.

But remember, SPV is about scalability. It means that it’ll work on a blockchain that has billions or even trillions of transactions in a single block. On such a scaled blockchain, scalable and efficient search becomes absolutely essential, for otherwise, everyone, including the sender, the recipient, and the service providers, will be at a loss.

So we need scalable search along with SPV. But what else can do this better than a binary search tree?

The binary search tree and SPV thus work together like a hand-in-glove. That is what BSV has done. The upcoming Teranode under testing is going to showcase these features. If you don’t care about a scalable system, you may not be excited to hear this. But that doesn’t mean you should puff up to claim that Dr. Wright is ignorant because he claims the Bitcoin Merkle tree is a binary search tree. To the contrary, you should find your own ignorance in failing to understand what he said.