|
Getting your Trinity Audio player ready...
|
This post was first published on Medium.
MiMC is a “ZK-friendly” hash function, for which efficient Zero Knowledge Proofs (ZKP) can be generated.
Previously, we discussed ZKP can be applied to any mathematical function using zk-SNARK. Internally, the function needs to be converted to a circuit, where only addition and multiplication operations are allowed. While all functions can be converted in theory, in practice some function’s circuit is smaller and their ZKP is less costly than those of others. For instance, SHA256 requires lots of bit operations and is thus among the most expensive in terms of circuit size.
The MiMC hash function is specifically designed to minimize circuit size and thus ZKP cost by using only additions and multiplications. It does not while making it extremely costly to reverse-engineer the pre-image of the hash.
Hash function can be found in many applications such as commitment scheme, signature, and Merkle trees. MiMC is a good candidate hash function when efficient ZKP is needed.
Algorithm
To hash a single number x, we calculate the following function:
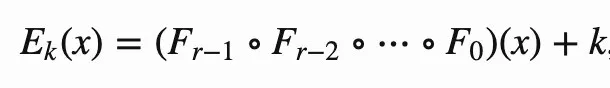
r is the number of rounds, Fᵢ is the round function for round i and k is the key. ∘ is function composition.
Fᵢ is defined as:
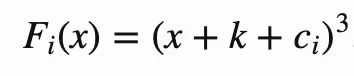
cᵢ are the round constants and c₀=0.
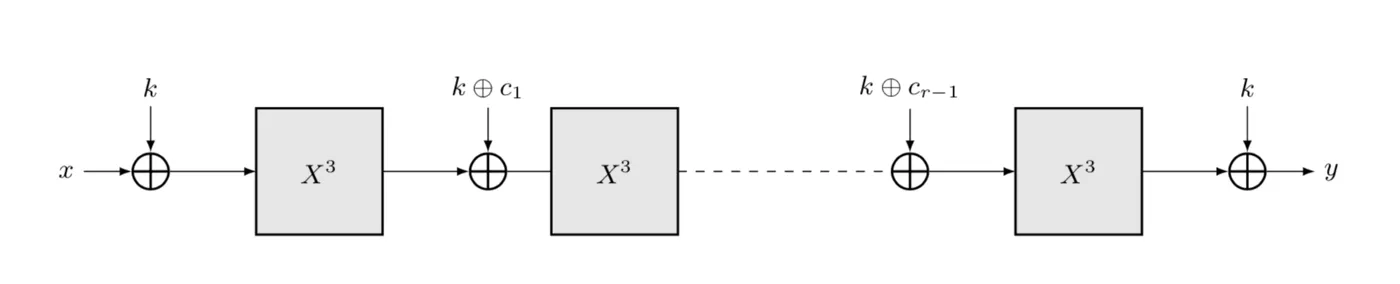
r rounds of MiMC: Eₖ(x)
Implementation
The following is an implementation of MiMC:
hash() at Line 1 computes Eₖ(x). multiHash() hashes an arbitrarily long input xs, where the intermediate result ret is fed into the next iteration at Line 17. All operations are defined in modular P.
A test can also be found here.
Watch: The BSV Global Blockchain Convention presentation, Smart Contracts and Computation on BSV
https://youtu.be/c_zAlkImgTU

 07-03-2025
07-03-2025 





