This post was first published on Medium.
A (t, n) threshold signature scheme (TSS) is a cryptographic protocol that allows a group of n participants to collectively sign documents or transactions, where any subset of t + 1 or more participants can produce a valid signature, but subsets of t or fewer cannot. This scheme is designed to enhance security and trust in distributed systems by ensuring that no single party can unilaterally generate a signature, thus preventing unauthorized actions. TSS enhances the security of cryptographic keys by splitting the control among multiple parties, where the key never exists.
Preliminary: Polynomial Interpolation
A polynomial of degree (t-1) is uniquely determined by t points. For example, two points define a line, three points a parabola, and so forth.
If all points are scaled by a constant factor, the interpolated polynomial is also scaled by the same factor. So is its y-intercept at x = 0.
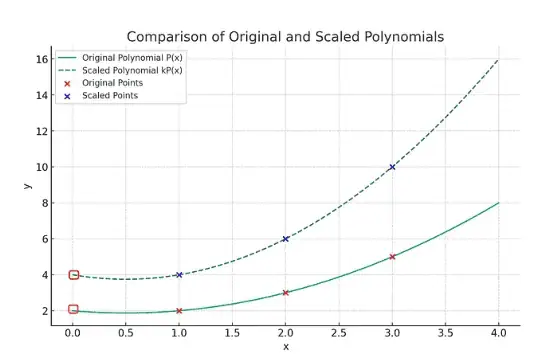
In the above example, you have a polynomial P(x) of degree 2 that fits points {(1,2), (2,3), (3,5)} and you scale the y-values by 2, you effectively scale P(x) by 2 to get the interpolation polynomial for {(1,4), (2,6), (3,10)}. Its y-intercept is also scaled by 2, from 2 to 4.
We will use this observation several times throughout the article.
Threshold Signature Schemes
Imagine a scenario with a group of n participants labeled as P₁ to Pₙ. In this setup, a (t, n) threshold signature scheme (TSS) grants the ability for any combination of t + 1 members to collaboratively produce a signature. However, any group smaller than or equal to t members lacks this ability.
TSS includes three phases.
1. Key Generation
Distributed Key Generation (DKG) protocol is used, as described in our previous post
Distributed Key Generation. The secret shared is a private key sk, which is unknown to any single party.
Assume that DKG is run by participants, denoted as P₁ through Pₙ, and results in each user Pᵢ receiving an individual secret share skᵢ, along with a shared public key pk for validation purposes. skᵢ represents a (t, n) Shamir secret share of the overall secret sk. Note that this key generation is a one-time initial setup phase for TSS, meaning that, once established, these private key shares are reusable for multiple operations.
The shared public key pk is the 0-intercept of the interpolation of all shares’ commitments (skᵢG), which are broadcast in the Verifiable Secret Sharing (VSS) phase. To see why, notice
pk = skG
G in the generator point and a constant. sk is 0-intercept of all skᵢ’s, thus pk is that of all skᵢG’s.
2. Signature Generation
Signature generation runs in two steps:
- Partial signature generation: Each participant produces a partial signature σᵢ using his share skᵢ on a message M: σᵢ = S(skᵢ, M), S being the signing function.
- Partial signature aggregation: Aggregating these partial signatures will produce a final signature σ. The most crucial thing is that the process ensures that the private key never appears, and thus, no leakage of secret can occur.
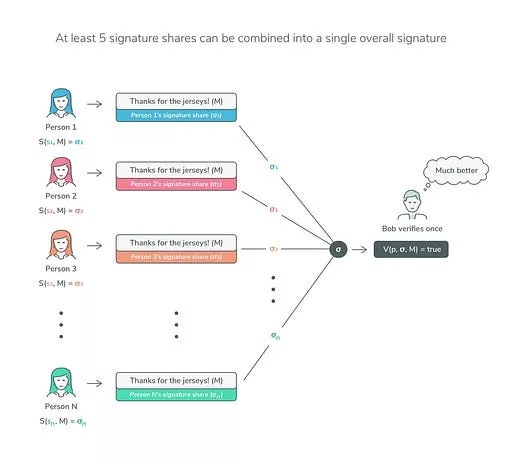
3. Signature Verification
The verification of a threshold signature scheme is identical to that of its non-threshold counterpart. Anyone with access to the public key and the message can verify the validity of the signature.
BLS Threshold Signatures
There are multiple signature schemes that can be extended to a threshold version, including ECDSA, Schnorr, and BLS. We chose BLS as an example for ease of exposition.
Key Generation
At the end of the threshold key generation, each user Pᵢ obtains a key share, skᵢ, and a common public key pk for verification.
Partial Signature Generation
This step is the same with non-threshold BLS.
ᵢ generates signature share as follows.
σᵢ = skᵢH(m)
m is the message and H is a cryptographic hash function.
Partial Signature Aggregation
A verifier first gathers 𝑡 different and valid partial BLS signatures, σᵢ , on 𝑚.
The difficulty here is how to get σ from σᵢ’s, without knowing sk.
σ = skH(m)
It turns out σ is the y-intercept of a Lagrange interpolation of all σᵢ’s.
This is because σᵢ is a constant factor of skᵢ, i.e., H(m), which is shared by all participants. Since sk is a y-intercept of a Lagrange interpolation of all skᵢ’s in DKG, σ is that of all σᵢ’s.
Verification
The aggregate signature σ is now a valid signature for m for the aggregate public key pk. Signature verification is the same as in the non-threshold version. A verifier checks the following equation:
e(H(m), pk) ?= e(σ, G)
pk is the aggregate public key and G is the generator point.
Comparisons
Threshold signatures are conceived from the integration of DKG and Multi-Signature (MultiSig) technologies, blending the superior features of each. This fusion results in a robust cryptographic solution that encapsulates the strengths of its predecessors.
TSS vs. Multisig
In contrast to multi-signature approaches, Threshold Signature Schemes (TSS) are recognized for generating more compact signatures while enhancing privacy protections. Furthermore, TSS inherently extends multi-signature functionalities to blockchain technologies that otherwise do not support these features directly, particularly in contexts requiring both efficiency and discretion. Crucially, TSS architectures avoid storing private keys on servers, thereby bolstering risk management and facilitating the division of responsibilities among participants. These prominent benefits position TSS as an optimal solution for the development of secure hot wallets that operate in real time without compromising the confidentiality of private keys.
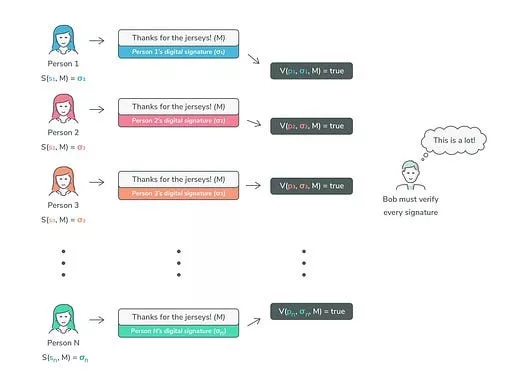
TSS vs. DKG
In DKG, a secret can be constructed if a quorum of participants collaborates with their shares. In the context of signatures, the secret is the private key. It can be created first and used for signing. However, this existence of private key in its entirely, even briefly, creates a single point of failure, making it vulnerable to attacks. In TSS, the private key never exists and no one ever sees the private key in plaintext at any point in the signing process, making it immune to such attacks.
Implementation
We have implemented a (3, 5)-threshold signature scheme on Bitcoin. We choose ECDSA version of TSS since ECDSA is natively supported in Bitcoin. It is based on the library tss-lib.
A single run results in the following transactions:
- Deployment Transaction ID: 3c0d8b44f8740a0c45162fa6bb6835808b9b04a884853fcb597af1a0812d6345
- Spend Transaction ID: cfc1704361367d902da142c3307c4d0ef9cfe6c6e5d882af258c3a1964ebe9b5
The address and signature look identical to the ones generated normally without using TSS.
Watch: sCrypt applications are proving how powerful Bitcoin is
New to blockchain? Check out CoinGeek’s Blockchain for Beginners section, the ultimate resource guide to learn more about blockchain technology.
