The first successful Zero-Knowledge Pay-to-Sudoku Bounty on Bitcoin

Getting your Trinity Audio player ready...

This post was first published on Medium.

We are excited to announce the first successful Zero-Knowledge Bounty on the Bitcoin network. We have applied Zero-Knowledge Bounty to solve a 9×9 Sudoku puzzle.

Compared to Pay-to-Sudoku using Zero-Knowledge Contingent Payment (ZKCP), a seller does not have to interact with the buyer, who only needs to post a single bounty transaction. More crucially, the buyer cannot abort after the seller has spent resources solving the puzzle and proven the solution is valid, and thus deprive the seller of payment by refusing to post a bounty transaction.

Circuit

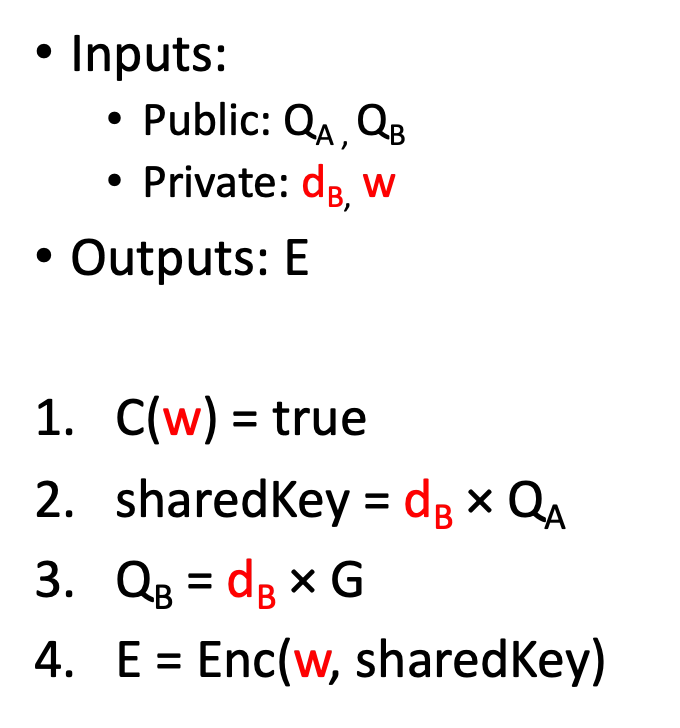
The circuit is an instantiation of the generic ZK bounty circuit. In step 1, the subcircuit C validates the Sudoku solution. In step 4, the ZKP-friendly Poseidon encryption is used.

Smart Contract

The bounty contract simply verifies the ZK proof at Line 20. If it is valid, it sends the bounty reward to the buyer, using OP_PUSH_TX, from Line 25 to 30.

SudokuBounty contract

Alice can reclaim the bounty if nobody claims it by the deadline at Line 33.

A working example

As in the general ZK bounty, there are three steps:

1. Alice places a bounty transaction Tm 8e524b7de2f42cf45daf2851e00161ee6984780c464e484b88b34bb6c629911f for the Sudoku puzzle in Line 22–32 of the circuit.
2. Bob solves the puzzle and encrypts the solution with a shared ECDH key. He generates a ZK proof and submits a transaction
   Tc 32b3b9906d4cdfe2aa5fe6aeec31d39d7b3040bf3d8548296cd7ad04f288fab1 to claim the bounty, containing the proof and the encrypted solution.
3. Using Tc, Alice derives the same shared key using her own private key and Bob’s public key in Tc’s output, decrypt the encrypted solution in Tc’s input to get the final solution.

Note there is no back-and-forth interaction between Alice and Bob and no trusted middleman involved. Also nobody else watching both transactions knows the solution since it is encrypted.

The full code can be found at this repo, with an end-to-end test and deployment.

Optimization: reduce number of public inputs

The on-chain ZKP verifier does a elliptic curve scalar multiplication for each public input of the circuit, which is rather expensive. We pass these inputs as private parameters to the circuit and only used their hash as a public input. Both the circuit and smart contract assert that hashing these inputs actually produces the specified hash. This approach reduces public inputs from 100 (each field of the Sudoku board needs its own input) down to only 2.

Watch: The BSV Global Blockchain Convention presentation, Smart Contracts and Computation on BSV