This post was first published on Medium.
We have implemented elliptic curve (EC) arithmetic in Script. In the previous implementation, we conduct the computation off chain and verify the result in Script. We compute directly in Script here.
There are numerous applications based on EC, especially in the field of cryptography, such as digital signatures, encryption, and commitment schemes. As a concrete example, we have reimplemented ECDSA signature verification that allows verifying signatures with arbitrary messages.
Modular Inverse
Before implementing point addition and multiplication, we introduce modular inverse since it is a building block.
A modular multiplicative inverse of an integer a is an integer x, such that a*x ≡ 1 mod n. In order to derive this value, we use the extended Euclidean algorithm (eGCD). Because modular inverse will take up most of the script size when using EC arithmetic, it is crucial to optimize it as much as possible. Thus, we use inline assembly to code it directly in raw Script.
Extended Euclidean Algorithm
The extended Euclidean algorithm is an extension to the standard Euclidean algorithm. In addition of finding the greatest common divisor (GCD), it also computes the coefficients of Bézout’s identity, which are integers x and y such that:
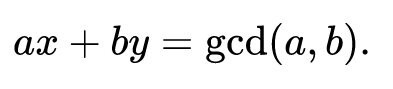
The eGCD algorithm is defined as follows:
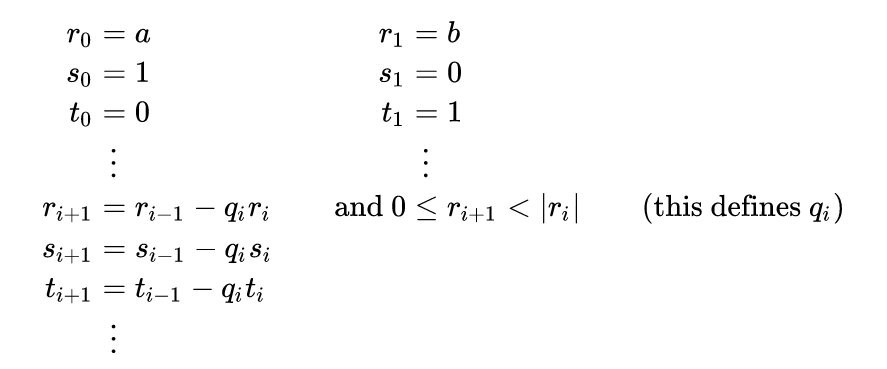
The execution stops when remainder r(i+1) is 0. If a and b are coprime (in the case of EC arithmetic they always should be, because curve parameters p and n are prime), x is also the modular inverse of a mod b.
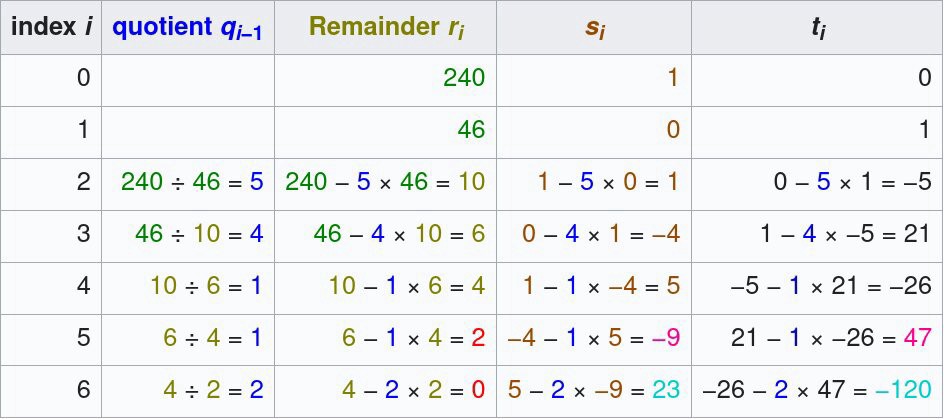
The following is an example calculation table of the eGCD algorithm with inputs a = 240 and b = 46:
Implementation
The following is a highly-optimized implementation of the extended Euclidean algorithm in Script. Because we are just interested in the t(i) sequence, we do not need to track the s(i) sequence and thus keep the script size smaller.
Calculating the upper bound of the loop
The upper bound of the number of iterations for a k-bit modulus n can be derived with the following equation:
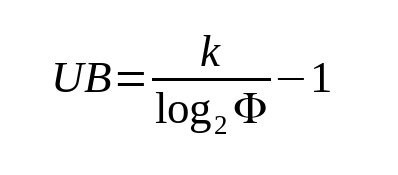
, where phi is the golden ratio:
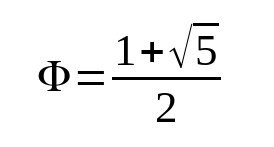
For a modulus of 256 bits, like the Bitcoin curve secp256k1, we get an upper bound of 368. The resulting script of modInverseEGCD() is about 7 KB in size.
Point addition
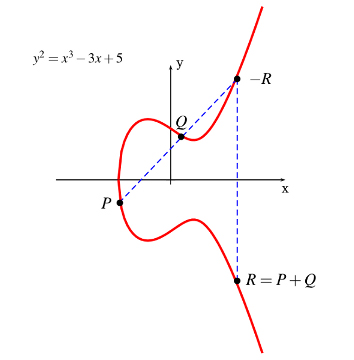
Point addition on an elliptic curve is defined as the negation of the curve intersection point of a straight line that goes through point P and Q. If one of the points is the point at infinity (0, 0), we just return the other point.
Point doubling
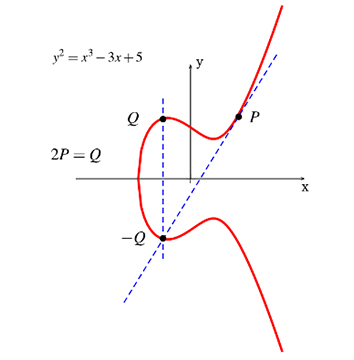
If P and Q are at the same coordinates we use the intersection of the tangent to the curve at that coordinate.
Scalar multiplication
Multiplication of point with a scalar is the most computationally intensive function we define. We used the double-and-add algorithm for simplicity. There are more efficient approaches.
ECDSA Signature Verification
Now that we have all the needed EC primitives implemented, we can define a function to check the validity of signatures over arbitrary messages, without any new opcode such as OP_CHECKSIGFROMSTACK on BTC or OP_DATASIGVERIFY (aka, OP_CHECKDATASIG) on BCH.
As we can see, the function calls scalar multiplication twice. A single call to multByScalar() costs us about 5 MB of script size. Hence a single signature verification is ~10 MB of script, which can be optimized further.
We could even use a custom curve instead of the standard secp256k1 and use a larger key size to improve security drastically.
Acknowledgements
This is an implementation of nChain whitepaper 1611.
New to blockchain? Check out CoinGeek’s Blockchain for Beginners section, the ultimate resource guide to learn more about blockchain technology.
