Zero-Knowledge proof of solvency for crypto exchanges: How to detect the next FTX and Mt. Gox

Getting your Trinity Audio player ready...

This post was first published on Medium.

The implosion of the cryptocurrency exchange FTX, with billions of customer funds missing, is the latest example of exchange insolvency in the history of cryptocurrencies. The history stretches all the way back to 2014 when the oldest and largest exchange Mt. Gox, handing 70% of bitcoin trades, lost 850,000 bitcoins of its users.

Many users today prefer to store their cryptocurrency asserts with centralized exchanges for ease of use similar to online banking, to avoid the difficulty and risk of managing cryptographic keys themselves.

Unfortunately, storing assets with an exchange exposes users to the risk of the exchange losing them due to external or internal theft.

We show a method for an exchange to cryptographically prove solvency, meaning its assets cover its liabilities. The proof does not disclose any private information, including its customers, addresses it controls, and total liabilities. The proposed methods can be complementary to trusted auditing, which can be costly, or be applied independently.

Naive approach

A rudimentary approach to for an exchange to demonstrate its solvency is to publicly disclose liabilities for all users and all Bitcoin addresses it controls. Any party can calculate its total liabilities and assets, thus check if it is fully solvent.

Each user can verify independently he is in the liability dataset. The exchange can be caught if it leaves out any user.

The exchange can prove its possession of the private key to any address, by digitally signing or moving the balance to a new address.

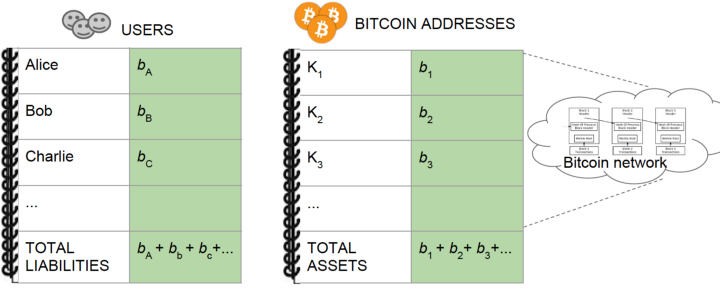
This approach of full transparency is obviously problematic since it leaks commercially sensitive information on the exchange and its users. We need a privacy-preserving alternative.

Cryptographic primitives

Pedersen commitments

The Pedersen commitment to a message x is defined as

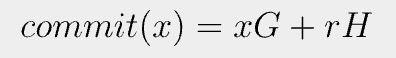
G and H are independent generators of an elliptic curve. r is a random value called the blinding factor.

In contrast with a hash-based commitment such as SHA256, Pedersen commitment is additively homomorphic. It means that without knowledge of the two values x and y, one can add their corresponding commitments to calculate a commitment to their sum.

Zero-Knowledge Range proof (ZKRP)

A ZKRP is a special type of Zero-Knowledge proof that shows a number lies within a certain range, without disclosing the number. Bulletproof is the an efficient ZKRP construction.

Proof of assets

In a proof of assets (aka, proof of reserves), an exchange acts as a prover of its total assets and any party can play the role of a verifier.

To prevent the exchange’s private data from leaking, the following measures are taken.

1. More anonymity addresses are added into the full asset set, whose private key the exchange does not know. This obfuscates the set of addresses possessed by the exchange.

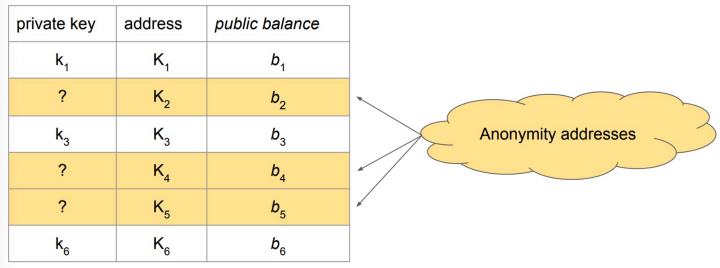
2. A ZKP such as zk-SNARK is used to prove the following statement for each address:

Either I know the private key corresponding to the address and the commitment is to the balance of the address

or

I don’t know the private key and the commitment is to the value 0.

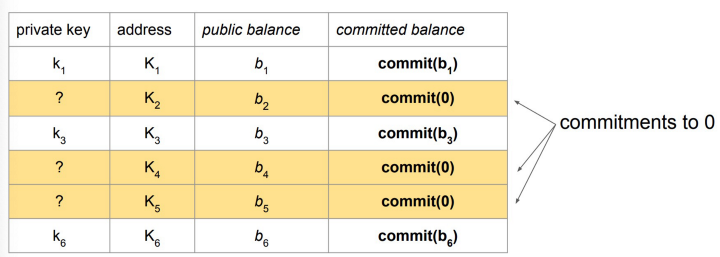
3. The total asset balance can be obtained by summing all individual commitments proved in Step 2. Note the total asset, which is proprietary and sensitive, is not disclosed, only its Pedersen commitment.

The final result is a Pedersen commitment to the total assets commit(assets) that the exchange knows private keys for a subset of Bitcoin addresses in the full set.

Proof of liabilities

Next, an exchange proves the total quantity of coins it owes to all of its customers. Each customer verifies it is included.

Summation Merkle tree

To do this, the exchange organizes all users into a variant of Merkle tree. Each leaf represents a user and her balance. Compared to a canonical Merkle tree, the summation Merkle tree makes two modifications.

1. Besides the hash, a balance field is added into each node. The balance of a node is the sum of its two children.
2. Instead of a hash such as SHA256, a Pedersen commitment is used.

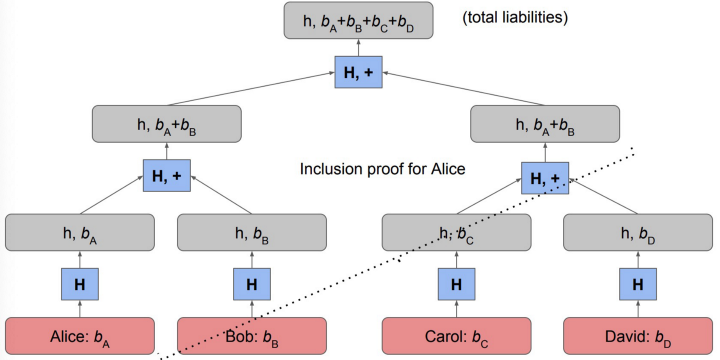
The root of the tree contains the commitment of the total liabilities. The exchange signs the root and publishes it on, e.g., Bitcoin.

Each customer can request a Merkle proof of their inclusion against the published root. If a sufficient number of customers verify independently, a cheating exchange can be caught with high probability.

Range proof

A dishonest exchange can cheat by including fake users with negative balance and thus reducing their total liabilities. To prevent this attack, the exchange also provides a ZKRP each customer at the leaf has a nonnegative balance, without disclosing the balance itself.

Note that the exchange is disincentivized to add fake users with positive balance, since it increases their liabilities.

Proof of solvency

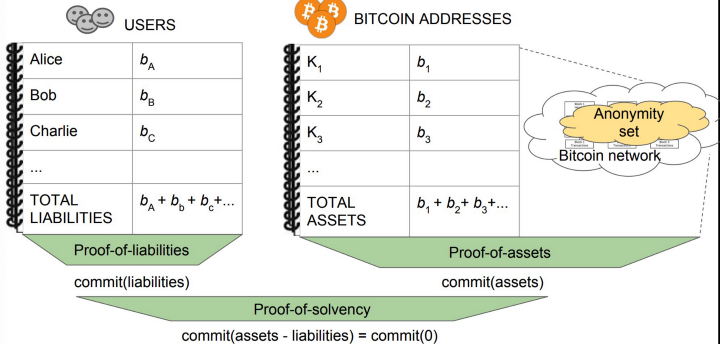
Once the exchange completes proof of assets and liabilities, we can calculate the commitment of its balance.

commit(balance) = commit(assets) — commit(liabilities)

The exchange has two ways to prove the balance is nonnegative, i.e., the exchange is solvent.

1. Open the commitment directly.
2. Prove the balance is nonnegative using ZKP, given its commitment.

Discussion

Our proof of solvency is only a preliminary step for exchanges to increase transparency and boost customer confidence. There are many other measures to be taken for it to be adopted in practice, where an exchange publishes the proof regularly.

For example, a cabal of insolvent exchanges can collude by covering each exchanges’ individual liabilities with their collective assets. In essence, there is nothing that prevents the assets of a single Bitcoin address from being used in the proof of solvency for various exchanges. To counter this attack, the proof of assets for an exchange needs to prove the set of addresses is disjoint from that of another exchange.

References

[1] Provisions Privacy-preserving proofs of solvency for Bitcoin exchanges Real World Crypto 2016: slides

[2] A ZK-SNARK based Proof of Assets Protocol for Bitcoin Exchanges

Watch: CoinGeek New York presentation, FYI: Better Information Tools for a More Lawful Blockchain Industry