|
Getting your Trinity Audio player ready...
|
This post was first published on Medium.
Smart contracts have no knowledge of the outside world and have to rely on oracles to import external data in general. We have shown two ways to import data from oracles before, based on Rabin signature and ECDSA. In this article, we show it is possible to access a specific type of external data, i.e., data on the blockchain (such as block headers and transactions), in the absence of oracles, while still maintaining data integrity. By allowing smart contracts to access on-chain data with minimal trust, it opens endless opportunities for all new kinds of smart contracts on Bitcoin.
Access block headers
The Bitcoin blockchain consists of a chain of blocks, as the name suggest. A block has two parts: a block header and transactions.
A block header contains the metadata of the block, with six fields as shown below.

It is worth noting that bitcoin headers are part of Bitcoin’s proof-of-work consensus algorithm. More specifically, the hash of a serialized block header should not exceed the difficulty target (i.e., the number of leading zeros). Thanks to trustless nature of proof of work, it is extremely costly to produce a valid block header, especially when the difficulty is high. But it is very easy to check if a given block header is valid. This is exactly how we import a block header into a smart contract shown below, without relying on any oracles.
Blockchain Contract
isBlockHeaderValid() at Line 22 checks if a block header is valid. bits2Target() at Line 31 calculates the difficulty target from a compact form (a 4-byte field typically referred to as nBits). We simply hash the block header at Line 23 and make sure it meets the difficulty target at Line 27.
Fake block headers
We also check the difficulty target is no larger than the blockchainTarget parameter at Line 27, to control the difficulty of producing a fake block header. Otherwise, an attacker can easily create a block header, whose hash meets the target of difficulty within (e.g., only has 2 leading zeros). As with many other aspects of Bitcoin such as 0-conf, the security of importing block headers this way is economic, not merely technical. This means in practice, it is imperative that a smart contract relying on a real block header should not lock more coins than it costs to produce a fake header.
Access transactions
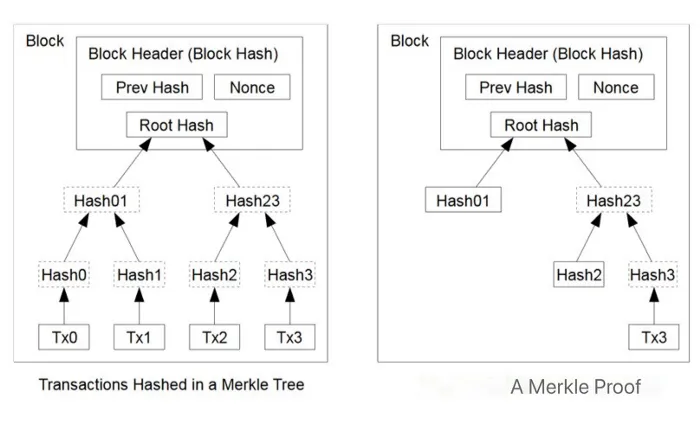
Once a block header is available, we can easily access any transaction in the block. This is because the block header contains the root of the Merkle tree of all the transactions. Similar to SPV, we pass the transaction and its Merkle path into a smart contract and verify it matches the root hash in the block header. txInBlock() at Line 17 demonstrates this.
A case study: Using blockchain to generate random numbers
In general, it is considered a hard problem to generate pseudo-random numbers in a blockchain securely and fairly, since the blockchain is both deterministic and transparent. We leverage blockchain data, specifically the nonce field of a block header, as the source of entropy.
Alice and Bob both lock same amount of bitcoins into the following contract. Once the transaction containing the contract is broadcasted, it will be mined into a future block. Depending on the nonce of the block, which is hard to predict and can be regarded as random, a winner is determined and takes all locked bitcoins.
BlockchainPRNG Contract
Line 17 and 20 use the OP_PUSH_TX technique to get the txid of the transaction containing the contract. Line 23 verifies the block header is legitimate and Line 26 verifies the previous transaction is in it. If the nonce field is odd, Alice wins; otherwise, Bob wins.
Summary
We have shown how to access blockchain data in Bitcoin smart contracts with minimal trust. Since a serialized bitcoin header is only 80-bytes long and Merkle proof scales logarithmically, this technique is extremely efficient (same as SPV).
We have also shown an example to use the blockchain data to generate pseudo-random numbers. This is only the beginning of what is possible, which we will explore in future posts. Stay tuned.
Acknowledgements
This work is inspired by the work of Ying Chen now at Cambridge Cryptographic.
Watch: CoinGeek New York presentation, Smart Contracts & Computation on Bitcoin

 07-02-2025
07-02-2025 





