Sign without knowing the private key in ECDSA

Getting your Trinity Audio player ready...

This post was first published on Medium.

We demonstrate how to generate a valid signature without knowing the private key using Elliptic Curve Digital Signature Algorithm (ECDSA).

ECDSA Signing

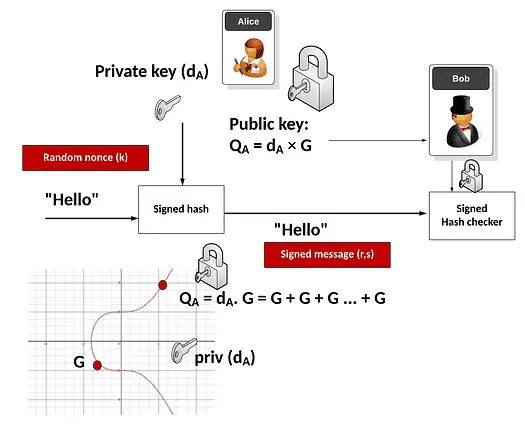
Alice thus has a private key (d) and a public key (Q = dG). She signs a message (m) with the following steps:

1. Hash the message: h = HASH(m).
2. Create a random number k and calculate R = kG. Find R’s x-coordinate r.
3. Calculate s = (h + rd)/k.

The signature is the pair (r, s). Both r and s are just scalar numbers.

Sign without knowing the private key

Conventionally, Alice has to know a private key to generate a valid signature against its public key. Remarkably, a valid signature can be generated without knowing the private key as follows:

1. Generate a random number r. If there is no point R on the curve with r as its x-coordinate, simply try another value of r.
2. Generate a random number s.
3. Solve for the public key as Q = (sR – hG)/r.

(r, s) is a valid signature for public key Q and message m. To see why, we can derive Q as follows:

s = (h + rd)/k
sk = h + rd
skG = hG + rdG
sR = hG + rQ
Q = (sR – hG)/r

We call Q a keyless public key, as it is not derived from a known private key. In contract, let us call a public key keyed if it is derived from a known private key, as typically done.

Note that a signature is generated first before a public key is derived, which is the opposite of a regular ECDSA signing.

Implications

If a public key is generated keylessly, only the person who generates it can produce a valid signature against it, with the signature and the message with hash h. The signature and the message jointly act as the private key here, which exists but is unknown. Note message hash h is used and thus committed in calculating Q, meaning the signature is only valid for m, but not for any other message. Both the signature and the message are needed for the signature to verify against the public key.

Keyless vs. keyed key

The private key of a keyed public key is known, while that of a keyless one is unknown. In a keyed scenario, the public key is known before the signature, while it is the opposite in a keyless one.

By looking at a public key alone, it cannot be determined if it is keyless or keyed.

Even if one signature is revealed for one message, it is impossible to decide if the public key is keyless or not since the signature can come from a private key or generated in advance.

However, if Alice can sign against a message chosen by Bob, it is overwhelmingly likely she knows the private key since she does not know the message committed in the public key in advance and cannot generate a valid signature.

If there are signatures for two different messages, even both chosen by Alice, we can be sure the public key is keyed.

Use in Bitcoin

It is alleged that the public key (denote as Q₀) in Bitcoin’s Genesis Coinbase transaction is keyless. If so, whoever possesses the signature can sign one message, the one used when calculating Q₀. He cannot sign any other message.

However, the signature is only valid off-chain, but not on-chain. Coins sent to that Q₀ cannot be spent with such a signature, including ones sent after the Genesis block¹. Too see why, we have to look at what message m is signed when creating a transaction. It basically includes the current spending transaction plus the output being spent. The output contains Q₀ in its script part, meaning m depends on Q₀. However, Q₀ itself depends on h, m’s hash. This circular dependency (to get Q₀, you need m first; but to get m, you need Q₀ first), similar to a signature that cannot sign itself in Bitcoin, prevents generating Q₀.

Note this applies to any public key in bitcoin, not only Q₀.

Implementation

Below is a full working example where a signature is generated without knowing the private key.

Anyone can run and independently verify it. A test run is shown below.

References

1. Blake, I.F., Seroussi, G. and Smart, N.P. (eds.) (2005) Advances in Elliptic Curve Cryptography. Cambridge: Cambridge University Press (London Mathematical Society Lecture Note Series).
2. Graph credit: Buchanan, William J (2024). Elliptic Curve Digital Signature Algorithm (ECDSA). Asecuritysite.com. https://asecuritysite.com/ecdsa/ecdsa2

***

[1] Coinbase output in the Genesis block cannot be spent even if the public key in it is keyed, since it is not included in the UTXO set. https://gist.github.com/msinkec/5eaf5aa97ed0f5e8d66e7e32fd8b1a0a

Watch: Digital identity, digital assets enable Web3